题目内容
8.让${\;}_{1}^{1}$H、${\;}_{1}^{2}$H、${\;}_{1}^{3}$H(质量相等,电荷数1:2:3)的混合物沿着与电场垂直的方向进入匀强偏转电场,要使它们的偏转角相同,这些粒子必须具有相同的( )| A. | 初速度 | B. | 初动能 | C. | 比荷 | D. | 质量 |
分析 带电粒子垂直进入匀强电场中,做类平抛运动,将粒子的运动进行正交分解,由牛顿第二定律、运动学以及两个分运动的等时性,得出偏转角的表达式,再进行分析.
解答 解:设带电粒子的质量为m,电量为q,匀强电场的场强大小为E,电场的宽度为L,初速度为v0,最后的偏转角为θ.
带电粒子在垂直电场方向做匀速直线运动,L=v0t,所以有:t=$\frac{L}{{v}_{0}}$,
沿电场方向做匀加速直线运动,加速度为:a=$\frac{qE}{m}$,
粒子离开电场时垂直于电场方向的分速度为:vy=at,
则有:tanθ=$\frac{{v}_{y}}{{v}_{0}}$,
解得:tanθ=$\frac{qEL}{m{v}_{0}^{2}}$,
${\;}_{1}^{1}$H、${\;}_{1}^{2}$H、${\;}_{1}^{3}$H的电量相等,质量不相等,要使θ相同时,则mv02相等,
初动能Ek0=$\frac{1}{2}$mv02相等,故B正确,ACD错误.
故选:B.
点评 带电粒子在电场中类平抛运动问题,研究方法与平抛运动相似,采用运动的分解法,由动力学方法进行研究.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.如图所示,通电螺线管左侧和内部分别静止吊一环a和b,当变阻器R的滑动头c向左滑动时( )
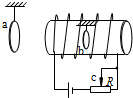

| A. | a向左摆,b向右摆 | B. | a向右摆,b向左摆 | C. | a向左摆,b不动 | D. | a向右摆,b不动 |
13.如图所示,两个大小相等互相绝缘的导体环,B环与A环有部分面积重叠,当开关S断开时( )
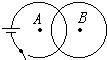
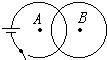
| A. | B环内有顺时针方向的感应电流 | B. | B环内有逆时针方向感应电流 | ||
| C. | B环内没有感应电流 | D. | 条件不足,无法判定 |
20.如图,在真空中把一绝缘导体向带负电的小球缓慢地靠近,下列说法中正确的是( )
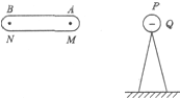

| A. | b端的感应电荷越来越少 | |
| B. | 导体内场强越来越大 | |
| C. | 导体的感应电荷在M点产生的场强恒大于在N点产生的场强 | |
| D. | 导体的感应电荷在M、N两点的场强相等 |
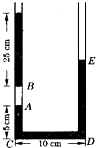 如图所示,截面均匀的U形玻璃细管两端都开口,玻璃管足够长,管内有两段水银柱封闭着一段空气柱,若气柱温度是27℃时,空气柱在U形管的左侧,A、B两点之间封闭着的空气柱长为15cm,U形管底边长CD=10cm,AC高为5cm.已知此时的大气压强为75cmHg.
如图所示,截面均匀的U形玻璃细管两端都开口,玻璃管足够长,管内有两段水银柱封闭着一段空气柱,若气柱温度是27℃时,空气柱在U形管的左侧,A、B两点之间封闭着的空气柱长为15cm,U形管底边长CD=10cm,AC高为5cm.已知此时的大气压强为75cmHg.
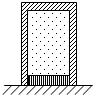 如图所示,质量为M的气缸用质量为m的活塞在缸内密封一定质量的理想气体,活塞跟缸壁间的摩擦不计,大气压为p0,活塞的横截面积为S,整个装置倒立在水平地面上.当封闭气体温度为T开时,活塞恰好跟地面接触,但没有受到地面对它的支持力.这时封闭气体的压强为${p_0}-\frac{mg}{S}$.当温度升高到某一值时,发现气缸恰好跟地面接触,但没有受到地面对它的支持力,这时封闭气体的温度为$\frac{{{p_0}S+Mg}}{{{p_0}S-mg}}T$.
如图所示,质量为M的气缸用质量为m的活塞在缸内密封一定质量的理想气体,活塞跟缸壁间的摩擦不计,大气压为p0,活塞的横截面积为S,整个装置倒立在水平地面上.当封闭气体温度为T开时,活塞恰好跟地面接触,但没有受到地面对它的支持力.这时封闭气体的压强为${p_0}-\frac{mg}{S}$.当温度升高到某一值时,发现气缸恰好跟地面接触,但没有受到地面对它的支持力,这时封闭气体的温度为$\frac{{{p_0}S+Mg}}{{{p_0}S-mg}}T$.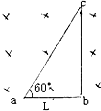 如图所示,一个直角三角形导线框放在匀强磁场中,磁场方向垂直线框平面指向纸内,磁感应强度为B,ab=L.当线框绕过b点的轴在纸面上顺时针以角速度ω转动时,线框中的感应电流大小为0,ca两点的电势差为φca=BL2ω.
如图所示,一个直角三角形导线框放在匀强磁场中,磁场方向垂直线框平面指向纸内,磁感应强度为B,ab=L.当线框绕过b点的轴在纸面上顺时针以角速度ω转动时,线框中的感应电流大小为0,ca两点的电势差为φca=BL2ω.