题目内容
 (2005?海淀区一模)如图所示,两根相距为d足够长的平行光滑金属导轨位于水平面的xoy平面内,一端接有阻值为R的电阻.在x>0的一侧存在竖直向下的匀强磁场,磁感应强度为B,一电阻为r的金属直杆与金属导轨垂直放置并接触良好,金属杆可在导轨上滑动.开始时,金属直杆位于x=0处,给金属杆一大小为v0、方向沿x轴正方向的初速度.在运动过程中有一大小可调节的外力F作用在金属杆上,使金属杆保持大小为a、方向沿x轴负方向的恒定加速度运动.金属轨道电阻忽略不计.
(2005?海淀区一模)如图所示,两根相距为d足够长的平行光滑金属导轨位于水平面的xoy平面内,一端接有阻值为R的电阻.在x>0的一侧存在竖直向下的匀强磁场,磁感应强度为B,一电阻为r的金属直杆与金属导轨垂直放置并接触良好,金属杆可在导轨上滑动.开始时,金属直杆位于x=0处,给金属杆一大小为v0、方向沿x轴正方向的初速度.在运动过程中有一大小可调节的外力F作用在金属杆上,使金属杆保持大小为a、方向沿x轴负方向的恒定加速度运动.金属轨道电阻忽略不计.(1)该回路中存在感应电流的时间多长?
(2)当金属杆的速度大小为v0/2时,回路中的电流有多大?
(3)若金属杆质量为m,试推导出外力F随时间t变化的关系.
分析:(1)由题得知,金属杆做匀变速运动,由运动学公式可求出存在感应电流的时间.
(2)根据法拉第电磁感应定律与闭合电路欧姆定律,可求出电流的大小.
(3)由牛顿第二定律与运动学公式,可列出外力与时间的关系式.
(2)根据法拉第电磁感应定律与闭合电路欧姆定律,可求出电流的大小.
(3)由牛顿第二定律与运动学公式,可列出外力与时间的关系式.
解答:解:(1)金属杆一大小为v0、方向沿x轴正方向的初速度.接着向右匀减速运动,当速度为零后,向左匀加速运动,
所以回路中存在感应电流的时间t=
,
(2)根据法拉第电磁感应电动势,则有E=
Bdv0,
由闭合电路欧姆定律,则有I=
,
(3)根据牛顿第二定律与运动学公式,
当金属杆向x正方向运动时,则有:F=ma-
+
(0≤t≤
)
当金属杆向x负方向运动时,则有:F=ma++
(
≤t≤
)
答:(1)该回路中存在感应电流的时间=
;
(2)当金属杆的速度大小为
时,回路中的电流有I=
;
(3)若金属杆质量为m,则推导出外力F随时间t变化的关系:当金属杆向x正方向运动时,则有:F=ma-
+
(0≤t≤
)
当金属杆向x负方向运动时,则有:F=ma++
(
≤t≤
).
所以回路中存在感应电流的时间t=
| 2v0 |
| a |
(2)根据法拉第电磁感应电动势,则有E=
| 1 |
| 2 |
由闭合电路欧姆定律,则有I=
| Bdv0 |
| 2(R+r) |
(3)根据牛顿第二定律与运动学公式,
当金属杆向x正方向运动时,则有:F=ma-
| B2d2v0 |
| R+r |
| B2d2at |
| R+r |
| v0 |
| a |
当金属杆向x负方向运动时,则有:F=ma++
| B2d2at |
| R+r |
| v0 |
| a |
| 2v0 |
| a |
答:(1)该回路中存在感应电流的时间=
| 2v0 |
| a |
(2)当金属杆的速度大小为
| v0 |
| 2 |
| Bdv0 |
| 2(R+r) |
(3)若金属杆质量为m,则推导出外力F随时间t变化的关系:当金属杆向x正方向运动时,则有:F=ma-
| B2d2v0 |
| R+r |
| B2d2at |
| R+r |
| v0 |
| a |
当金属杆向x负方向运动时,则有:F=ma++
| B2d2at |
| R+r |
| v0 |
| a |
| 2v0 |
| a |
点评:本题是电磁感应与运动学和动力学知识的综合应用,要防止只研究金属杆沿x轴正方向运动过程,造成漏解.

练习册系列答案
相关题目
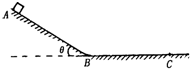 (2005?海淀区一模)如图,一物块从倾角为θ的斜面上A点由静止开始滑下,最后停在水平面上C点处.已知斜面与水平面的材料质地完全相同,已知物块在斜面和水平面上滑行的长度之比L1/L2=k,且斜面AB与水平面BC平滑相接.求:
(2005?海淀区一模)如图,一物块从倾角为θ的斜面上A点由静止开始滑下,最后停在水平面上C点处.已知斜面与水平面的材料质地完全相同,已知物块在斜面和水平面上滑行的长度之比L1/L2=k,且斜面AB与水平面BC平滑相接.求: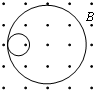 (2005?海淀区一模)在匀强磁场中有一个原来静止的碳14原子核,他放射出一个粒子,此粒子的径迹与反冲核的径迹是两个相内切的圆,大圆与小圆的直径之比为7:1,如图所示,那么碳14原子核的衰变方程是哪一个( )
(2005?海淀区一模)在匀强磁场中有一个原来静止的碳14原子核,他放射出一个粒子,此粒子的径迹与反冲核的径迹是两个相内切的圆,大圆与小圆的直径之比为7:1,如图所示,那么碳14原子核的衰变方程是哪一个( ) (2005?海淀区一模)如图所示,用绝缘细绳悬吊一质量为m、电荷量为-q的小球,在空间施加一水平方向的匀强电场,使小球保持静止时细线与竖直方向成θ角,则电场强度的大小和方向为( )
(2005?海淀区一模)如图所示,用绝缘细绳悬吊一质量为m、电荷量为-q的小球,在空间施加一水平方向的匀强电场,使小球保持静止时细线与竖直方向成θ角,则电场强度的大小和方向为( ) (2005?海淀区一模)波速均为v=1.2m/s的甲、乙两列简谐横波都沿x轴正方向传播,某时刻波的图象分别如图所示,其中质点P在平衡位置,质点Q处于波峰.关于这两列波,下列说法正确的是( )
(2005?海淀区一模)波速均为v=1.2m/s的甲、乙两列简谐横波都沿x轴正方向传播,某时刻波的图象分别如图所示,其中质点P在平衡位置,质点Q处于波峰.关于这两列波,下列说法正确的是( )