题目内容
如图所示，一平板小车静止在光滑水平面上，质量均为m的物体A、B分别以2v0和v0的初速度，沿同一直线同时同向水平滑上小车，刚开始滑上小车的瞬间，A位于小车的最左边，B位于距小车左边l处.设两物体与小车间的动摩擦因数均为μ，小车的质量也为m，最终物体A、B都停在小车上.求：
（l）最终小车的速度大小是多少?方向怎样？
（2）若要使物体A、B在小车上不相碰，刚开始时A、B间的距离l至少多长？
解：（1）设小车最终的速度是v，由动量守恒可得：
m·2v0+ m·v0=3 m·v ① （2分）
由①式解得：v=v0 方向水平向右 ②（2分）
（2）A、B同时滑上小车后，它们均做匀减速直线运动．当B减速到与小车的速度相同时，B与小车相对静止，此后A继续做匀减速直线运动，B与小车做匀加速直线运动，直至它们达到相同的速度v0，设刚开始时A、B间的距离l．
由答图可知：B与小车相对静止时的共同速度是vB1，此时A的速度是vA1，由运动学知识和动量守恒可得：
m·2v0+ m·v0=2 m·vB1+ m·vA1 ③（2分）
在B停止运动前，A、B所受的滑动摩擦力fA= fB，它们的加速度aA1= aB1，此时小车所受的力：F=-2fA ④
小车的加速度：a= -2 aA1= -2 aB1 ⑤ （2分）
由答图可知：
⑥（2分）
⑦ （2分）
由⑥⑦式解得：
⑧
t1=
⑨
由图可知：
⑩（2分）
由⑧⑨式解得：
当B与小车相对静止，此后A在小车上相对小车移动的距离是lx，由能量守恒定律可知：
=μmglx 
（2分）
由以上式子解得：lx=
在t1前，A、B移动的位移分别是sA1、sB1，由图可知：
s= sA1-sB1=（2v0-v0）·t1 
（1分）
由⑨式解得：s= 
所以：l= s + lx 
（1分）
由上式解得：l=
（1分）
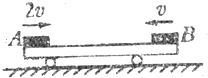如图所示，一平板小车静止在光滑的水平面上，质量均为m的物体A、B分别以2v和v的初速度、沿同一直线同时从小车两端相向水平滑上小车．设两物体与小车间的动摩擦因数均为μ，小车质量也为m，最终物体A、B都停在小车上（若A、B相碰，碰后一定粘在一起）求：
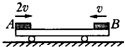如图所示，一平板小车静止在光滑的水平面上，质量均为m的物体A、B分别以2v和v的初速度、沿同一直线同时从小车两端相向水平滑上小车．设两物体与小车间的动摩擦因数均为μ，小车质量也为m，最终物体A、B都停在小车上（若A、B相碰，碰后一定粘在一起）．求：
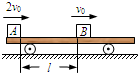如图所示，一平板小车静止在光滑水平面上，质量均为m的物体A、B分别以2v0和v0的初速度，沿同一直线同时同向水平滑上小车，刚开始滑上小车的瞬间，A位于小车的最左边，B位于距小车左边l处．设两物体与小车间的动摩擦因数均为μ，小车的质量也为m，最终物体A、B都停在小车上．求：
，小车质量也为m，最终物体A、B都停在小车上（若A、B相碰，碰后一定粘在一起）．求：