题目内容
 如图所示,一平板小车静止在光滑的水平面上,质量均为m的物体A、B分别以2v和v的初速度、沿同一直线同时从小车两端相向水平滑上小车.设两物体与小车间的动摩擦因数均为μ,小车质量也为m,最终物体A、B都停在小车上(若A、B相碰,碰后一定粘在一起).求:
如图所示,一平板小车静止在光滑的水平面上,质量均为m的物体A、B分别以2v和v的初速度、沿同一直线同时从小车两端相向水平滑上小车.设两物体与小车间的动摩擦因数均为μ,小车质量也为m,最终物体A、B都停在小车上(若A、B相碰,碰后一定粘在一起).求:(1)最终小车的速度大小是多少,方向怎样?
(2)要想使物体A、B不相碰,平板车的长度至少为多长?
(3)接(2)问,求平板车达到(1)问最终速度前的位移?
分析:(1)以A、B两物体及小车组成的系统为研究对象,由动量守恒定律可以求出它们的共同速度.
(2)应用动能定理求出小车的位移.
(2)应用动能定理求出小车的位移.
解答:解:(1)以A、B两物体及小车组成的系统为研究对象,
以A的初速度方向为正方向,由动量守恒定律得:
m?2v-mv+0=3mv′,解得:v′=
,方向向右.
(2)由能量守恒定律得:
m(4v)2+
mv2-
?3m(
)2=μmgL,则L=
;
(3)①物体A、B未相碰撞,B停止时,A继续运动,此时小车开始运动.对小车应用动能定理
μmgs=
?2m(
)2,则s=
;
②物体B速度为零时正好与A相撞,碰后小车开始加速,最终达到共同速度v共=
.
对小车应用动能定理得:μ?2mgs′=
m(
)2,则s′=
;
所以小车位移大小的取值范围是
≤s≤
;
速度达到
时的位移为
;
答:(1)最终小车的速度大小是
,方向向右.
(2)平板车的长度至少为则L=
.
(3)最终速度前的位移
.
以A的初速度方向为正方向,由动量守恒定律得:
m?2v-mv+0=3mv′,解得:v′=
| v |
| 3 |
(2)由能量守恒定律得:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| v |
| 3 |
| 7v2 |
| 3μg |
(3)①物体A、B未相碰撞,B停止时,A继续运动,此时小车开始运动.对小车应用动能定理
μmgs=
| 1 |
| 2 |
| v |
| 3 |
| v2 |
| 9μg |
②物体B速度为零时正好与A相撞,碰后小车开始加速,最终达到共同速度v共=
| v |
| 3 |
对小车应用动能定理得:μ?2mgs′=
| 1 |
| 2 |
| v |
| 3 |
| v2 |
| 36μg |
所以小车位移大小的取值范围是
| v2 |
| 36μg |
| v2 |
| 9μg |
速度达到
| v |
| 3 |
| v2 |
| 36μg |
答:(1)最终小车的速度大小是
| v |
| 3 |
(2)平板车的长度至少为则L=
| 7v2 |
| 3μg |
(3)最终速度前的位移
| v2 |
| 36μg |
点评:熟练应用动量守恒定律、动能定理是正确解题的关键;解题时要分析清楚运动过程.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
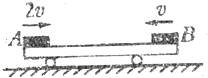 如图所示,一平板小车静止在光滑的水平面上,质量均为m的物体A、B分别以2v和v的初速度、沿同一直线同时从小车两端相向水平滑上小车.设两物体与小车间的动摩擦因数均为μ,小车质量也为m,最终物体A、B都停在小车上(若A、B相碰,碰后一定粘在一起)求:
如图所示,一平板小车静止在光滑的水平面上,质量均为m的物体A、B分别以2v和v的初速度、沿同一直线同时从小车两端相向水平滑上小车.设两物体与小车间的动摩擦因数均为μ,小车质量也为m,最终物体A、B都停在小车上(若A、B相碰,碰后一定粘在一起)求: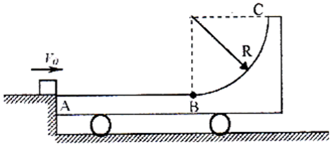
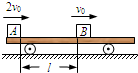 如图所示,一平板小车静止在光滑水平面上,质量均为m的物体A、B分别以2v0和v0的初速度,沿同一直线同时同向水平滑上小车,刚开始滑上小车的瞬间,A位于小车的最左边,B位于距小车左边l处.设两物体与小车间的动摩擦因数均为μ,小车的质量也为m,最终物体A、B都停在小车上.求:
如图所示,一平板小车静止在光滑水平面上,质量均为m的物体A、B分别以2v0和v0的初速度,沿同一直线同时同向水平滑上小车,刚开始滑上小车的瞬间,A位于小车的最左边,B位于距小车左边l处.设两物体与小车间的动摩擦因数均为μ,小车的质量也为m,最终物体A、B都停在小车上.求: