题目内容
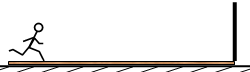 (2011?淮南一模)如图所示,长12m、质量为50kg的木板右端有一立柱,木板置于水平地面上,木板与地面间的摩擦因数为0.1,质量为50kg的人立于木板的左端.木板与人都静止.当人以4m/s2的加速度向右奔跑至板的右端时,立即抱住立柱.取g=10m/s2.试求:
(2011?淮南一模)如图所示,长12m、质量为50kg的木板右端有一立柱,木板置于水平地面上,木板与地面间的摩擦因数为0.1,质量为50kg的人立于木板的左端.木板与人都静止.当人以4m/s2的加速度向右奔跑至板的右端时,立即抱住立柱.取g=10m/s2.试求:(1)人在奔跑过程中受到的摩擦力的大小?
(2)人在奔跑的过程中木板的加速度.
(3)人从开始奔跑至到达木板的右端时,人和木板对地各运动了多大距离?
分析:(1)对人由牛顿第二定律即可求得所受摩擦力;
(2)由牛顿第三定律可知人对木板的摩擦力大小等于人所受摩擦力大小,对木板运用牛顿第二定律即可求出加速度;
(3)设人从左端跑到右端时间为t,由运动学公式求出各自的位移表达式,根据位移之和等于L即可求解.
(2)由牛顿第三定律可知人对木板的摩擦力大小等于人所受摩擦力大小,对木板运用牛顿第二定律即可求出加速度;
(3)设人从左端跑到右端时间为t,由运动学公式求出各自的位移表达式,根据位移之和等于L即可求解.
解答:解:(1)设人的质量为m,加速度为a1,人受的摩擦力为f,由牛顿第二定律有:
f=ma1=200N
(2)由牛顿第三定律可知人对木板的摩擦力大小f′=200N
设木板的质量为M,加速度为a2,对木板由牛顿第二定律有:
f′-μ(M+m)g=Ma2
代入数据得a2=2m/s2
(3)设人从左端跑到右端时间为t,由运动学公式:
L=
a1t2+
a2t2
解得:t=2s
人对地前进的距离 s1=
a1t2=8m
木板后退的距离为s2=
a2t2=4m
答:(1)人在奔跑过程中受到的摩擦力的大小为200N;
(2)人在奔跑的过程中木板的加速度为2m/s2;
(3)人从开始奔跑至到达木板的右端时,人运动的位移为8m,木板运动的位移为4m.
f=ma1=200N
(2)由牛顿第三定律可知人对木板的摩擦力大小f′=200N
设木板的质量为M,加速度为a2,对木板由牛顿第二定律有:
f′-μ(M+m)g=Ma2
代入数据得a2=2m/s2
(3)设人从左端跑到右端时间为t,由运动学公式:
L=
| 1 |
| 2 |
| 1 |
| 2 |
解得:t=2s
人对地前进的距离 s1=
| 1 |
| 2 |
木板后退的距离为s2=
| 1 |
| 2 |
答:(1)人在奔跑过程中受到的摩擦力的大小为200N;
(2)人在奔跑的过程中木板的加速度为2m/s2;
(3)人从开始奔跑至到达木板的右端时,人运动的位移为8m,木板运动的位移为4m.
点评:本题主要考查了牛顿第二定律的直接应用,要抓住人与木板的位移关系求解,难度适中.

练习册系列答案
相关题目
 (2011?淮南一模)为了研究过山车的原理,物理小组提出了下列的设想:取一个与水平方向夹角为37°、长为L=2.0m的粗糙的倾斜轨道AB,通过水平轨道BC与竖直圆轨道相连,出口为水平轨道DE,整个轨道除AB段以外都是光滑的.其中AB与BC轨道以微小圆弧相接,如图所示.一个小物块以初速度v0=4.0m/s,从某一高处水平抛出,到A点时速度方向恰沿AB方向,并沿倾斜轨道滑下.已知物块与倾斜轨道的动摩擦因数μ=0.5(g取10m/s2,sin37°=0.6,cos37°=0.8)求:
(2011?淮南一模)为了研究过山车的原理,物理小组提出了下列的设想:取一个与水平方向夹角为37°、长为L=2.0m的粗糙的倾斜轨道AB,通过水平轨道BC与竖直圆轨道相连,出口为水平轨道DE,整个轨道除AB段以外都是光滑的.其中AB与BC轨道以微小圆弧相接,如图所示.一个小物块以初速度v0=4.0m/s,从某一高处水平抛出,到A点时速度方向恰沿AB方向,并沿倾斜轨道滑下.已知物块与倾斜轨道的动摩擦因数μ=0.5(g取10m/s2,sin37°=0.6,cos37°=0.8)求:
 (2011?淮南一模)如图所示,一个质量m=0.5kg的小球(视为质点)从H=12m高处,由静止开始沿光滑弧形轨道AB滑下,接着进入半径R=4m的竖直圆环,当到达环顶C时,刚好对轨道压力为零;小在球沿左半环CB滑下后,再进入光滑弧形轨道BD,且到达D点时速度为零.g取10m/s2,下列说法正确的是( )
(2011?淮南一模)如图所示,一个质量m=0.5kg的小球(视为质点)从H=12m高处,由静止开始沿光滑弧形轨道AB滑下,接着进入半径R=4m的竖直圆环,当到达环顶C时,刚好对轨道压力为零;小在球沿左半环CB滑下后,再进入光滑弧形轨道BD,且到达D点时速度为零.g取10m/s2,下列说法正确的是( )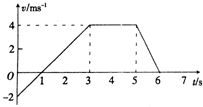 (2011?淮南一模)如图是质量为2.0kg的物体在水平面上运动的v~t图象,以水平向右的方向为正方向.以下判断正确的是( )
(2011?淮南一模)如图是质量为2.0kg的物体在水平面上运动的v~t图象,以水平向右的方向为正方向.以下判断正确的是( )