题目内容
如图所示，轻弹簧的一端固定，另一端与滑块B相连，B静止在水平导轨上，弹簧处在原长状态。滑块A从半径为R的光滑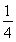
圆弧槽无初速滑下，从P点滑上水平导轨，当A滑过距离sl＝R时，与B相碰，碰撞时间极短，碰后A、B紧贴在一起运动，但互不粘连．最后A恰好返回出发点P并停止．在A、B压缩弹簧过程始终未超过弹簧的弹性限度。已知滑块A和B质量均为m（A、B可视为质点），且与导轨的滑动摩擦因数都为
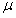＝0.1，重力加速度为g，试求：
（1）滑块A从圆弧滑到P点时对导轨的压力，
（2）A、B碰后瞬间滑块A的速度，
（3）运动过程中弹簧最大形变量S2
【答案】
(1)3mg? （2）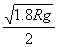
?? （3）0.625R
【解析】
试题分析：(1)设滑块A到达P点的速度为v0
由机械能守恒得:
???? ①? （2分）
在P点有：N-mg=
? ②?? （2分）
联立①②式得 N=3mg ③??? （1分）
由牛顿第三定律可知：
滑块A对导轨的压力
④? （1分）
（2）A刚接触B时速度为v1（碰前），A运动 s1过程由动能定理得，
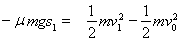?? ⑤? （2分）
碰撞过程中动量守恒,令碰后瞬间A、B共同运动的速度为v2，则有
m v1 =2m v2??? ⑥? （2分）
解得v2=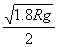?? ⑦? （2分）
（3）设A、B在弹簧碰后恢复到原长时, 共同速度为v3，在这过程中，由动能定理，有
?? ⑧?? （2分）
后A、B开始分离，A单独向右滑到P点停下，由动能定理有
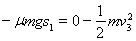? ⑨???? （2分）
解得? s2=0.625R?? ⑩??? （2分）
考点：本题考查牛顿运动定律、机械能守恒
练习册系列答案
阅读快车系列答案
相关题目
如图所示，轻弹簧的一端固定在竖直墙上，光滑弧形槽固定在光滑的水平面上，弧形槽底端与水平面相切，一质量为m的小物块从槽高h处开始自由下滑，下列说法正确的是（ ）
如图所示，轻弹簧的上端悬挂在天花板上，下端挂一质量为m的小球，小球处于静止状态．现在小球上加一竖直向上的恒力F使小球向上运动，小球运动的最高点与最低点之间的距离为H，则此过程中（g为重力加速度，弹簧始终在弹性限度内）（ ）
（2008?湛江二模）如图所示，轻弹簧的一端固定，另一端与滑块B相连，B静止在水平导轨上，弹簧处在原长状态．另一质量与B相同滑块A，从导轨上的P点以初速度v0向B滑行，当A滑过l1的距离时，与B相碰，碰撞时间极短，碰后A、B紧贴在一起运动，但互不粘连．已知滑块A和B皆可看作质点，且滑块A和B与导轨的滑动摩擦因数都为μ，运动过程中弹簧最大形变量为l2，求：
如图所示，轻弹簧的左端固定，右端与质量为m的物块B相连，B静止在粗糙水平面上的O点，此时弹簧处于原长．另一质量与B相同的物块A从P点以速度v0开始向B滑行，当A滑过距离l时，与B发生正碰，碰撞时间极短，碰后A、B粘在一起向左运动，A、B压缩弹簧后恰好能够返回并停在O点． 设A和B均可视为质点，它们与水平面的动摩擦因数均为μ．重力加速度为g．求：
如图所示，轻弹簧的一端固定，另一端与滑块B相连，B静止在水平导轨上的O点，此时弹簧处于原长．另一质量与B相同的块A从导轨上的P点以初速度v0向B滑行，当A滑过距离l时，与B相碰．碰撞时间极短，碰后A、B粘在一起运动．设滑块A和B均可视为质点，与导轨的动摩擦因数均为μ．重力加速度为g．求：