题目内容
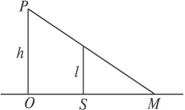
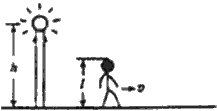
一路灯距地面的高度为h,身高为l的人以速度v匀速行走,如图所示。
(1)试证明人的头顶的影子作匀速运动;
(2)求人影的长度随时间的变化率。
(1)试证明人的头顶的影子作匀速运动;
(2)求人影的长度随时间的变化率。
解:(1)设t=0时刻,人位于路灯的正下方O处,在时刻t,人走到S处,根据题意有:
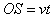 ①
①
过路灯P和人头顶做直线与地面的交点为M,M为t时刻人头顶影子的位置,如图所示:
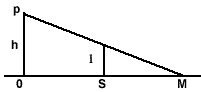
OM为人头顶影子到O点的距离,由几何关系,有:
 ②
②
联立①、②解得: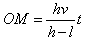 ③
③
因OM与时间t成正比,故人头顶的影子做匀速运动
(2)由图可知,在时刻t,人影的长度为SM,由几何关系,有:
SM=OM-OS ④
由①、③、④式解得: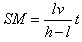 ⑤
⑤
可见影长SM与时间t成正比,所以影长随时间的变化率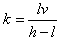 ⑥
⑥
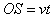 ①
① 过路灯P和人头顶做直线与地面的交点为M,M为t时刻人头顶影子的位置,如图所示:

OM为人头顶影子到O点的距离,由几何关系,有:
 ②
② 联立①、②解得:
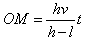 ③
③ 因OM与时间t成正比,故人头顶的影子做匀速运动
(2)由图可知,在时刻t,人影的长度为SM,由几何关系,有:
SM=OM-OS ④
由①、③、④式解得:
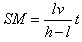 ⑤
⑤ 可见影长SM与时间t成正比,所以影长随时间的变化率
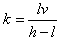 ⑥
⑥ 
练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
 (2005?福建模拟)一路灯距地面的高度为h,身高为l的人以速度v匀速行走,如图所示.
(2005?福建模拟)一路灯距地面的高度为h,身高为l的人以速度v匀速行走,如图所示. 一路灯距地面的高度为h,身高为l的人以速度υ匀速直线行走,如图所示.
一路灯距地面的高度为h,身高为l的人以速度υ匀速直线行走,如图所示.