题目内容
在绝缘水平面上,有两个质量各为m的绝缘小球A、B,二者相距S0,如图所示。已知A球光滑,带有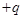 的电荷,B球与水平面间的动摩擦因数为
的电荷,B球与水平面间的动摩擦因数为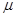 。现在水平面上方加一水平向右的匀强电场,电场强度为E,A、B两球将发生完全弹性碰撞,碰撞过程电荷不转移。(重力加速度为g)
。现在水平面上方加一水平向右的匀强电场,电场强度为E,A、B两球将发生完全弹性碰撞,碰撞过程电荷不转移。(重力加速度为g)
试求: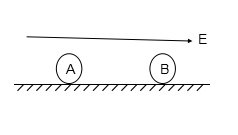
①A与B碰前的瞬间A球的速度。
②碰后瞬间A、B两球的速度各为多大?
③A、B两球从发生第一次碰撞到第二次碰撞时,A球通过的距离。
①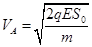 ②
②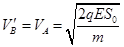 ③当
③当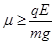 时,
时,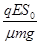 ;当
;当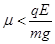 时,
时,
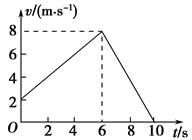
解析试题分析:①设A与B碰前的瞬间A球的速度为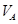 ,此段时间内利用动能定理得:
,此段时间内利用动能定理得: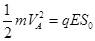 ,解得
,解得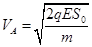 ①
①
②设碰后瞬间A、B两球的速度分别为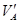 和
和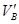 ,由于碰撞过程中动量和动能都守恒,故有:
,由于碰撞过程中动量和动能都守恒,故有: ②
② 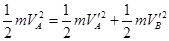 ③
③
联合①②③得: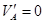 ,
,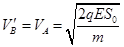 ④
④
③A、B两球碰撞后,在最初的一段时间内,A球在电场力作用下做初速度为零的匀加速运动,加速度大小为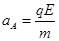 ⑤
⑤
B球在摩擦力的作用下做初速度为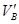 的匀减速运动,加速度大小为
的匀减速运动,加速度大小为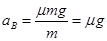 ⑥
⑥
要计算A、B两球从发生第一次碰撞到第二次碰撞A球通过的距离,有两种情况:一是B球的加速度过大,B球先停止,后A球与之碰撞;另一种情况是B球的加速度过小,在B球没有停止之前,A、B两球就已经发生了碰撞。
当B球刚停止二者刚好相碰时有: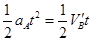 ⑦,
⑦,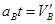 ⑧
⑧
联立 ④~⑧得: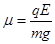 ⑨
⑨
于是:
ⅰ、当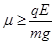 时,从发生第一次碰撞到第二次碰撞A球通过的距离等于B球减速的距离,
时,从发生第一次碰撞到第二次碰撞A球通过的距离等于B球减速的距离,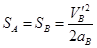 ⑩
⑩
联立④⑥⑩得:从发生第一次碰撞到第二次碰撞A球通过的距离为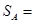
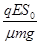
ⅱ、当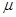 <
<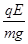 时,从发生第一次碰撞到第二次碰撞A球通过的距离就等于A球对B球的运动追击距离。设追击时间为
时,从发生第一次碰撞到第二次碰撞A球通过的距离就等于A球对B球的运动追击距离。设追击时间为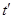 ,则
,则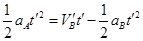 ,易求的
,易求的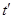 =
=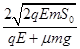
于是从发生第一次碰撞到第二次碰撞A球通过的距离为: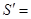
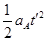 =
=
考点:动能定理,动量守恒定律,能量守恒定律,牛顿运动定律与运动学规律的综合应用

练习册系列答案
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
 ,在传送带将小物体从A点传送到B点的过程中,求:(g取10 m/s2)
,在传送带将小物体从A点传送到B点的过程中,求:(g取10 m/s2)

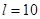 m,质量
m,质量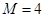 kg,放在光滑的水平面上.在A上最右端放一物块B(大小可忽略),其质量m=2kg.已知A、B间动摩擦因数
kg,放在光滑的水平面上.在A上最右端放一物块B(大小可忽略),其质量m=2kg.已知A、B间动摩擦因数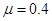 ,开始时A、B都处于静止状态(取
,开始时A、B都处于静止状态(取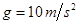 ).则
).则
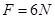 时,平板A与物块B的加速度大小各为多少?
时,平板A与物块B的加速度大小各为多少? 至少为多大?
至少为多大?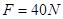 时,要使物块B从平板A上掉下来
时,要使物块B从平板A上掉下来 L,其中L为斜面长.求:滑块在斜面上滑行的时间t和斜面的长度L.
L,其中L为斜面长.求:滑块在斜面上滑行的时间t和斜面的长度L.