Question

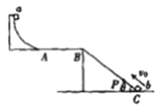
【题目】如图所示，竖直平面内有一四分之一光滑圆弧轨道固定在水平桌面AB上，轨道半径R=1.8m，末端与桌面相切于A点，倾角θ= 37°的斜面BC紧靠桌面边缘固定，从圆弧轨道最高点由静止释放一个质量m= lkg的可视为质点的滑块a，当a运动到B点时，与a质量相同的另一可视为质点的滑块b从斜面底端C点以初速度v0=5m/s沿斜面向上运动，b运动到斜面上的P点时，a 恰好平抛至该点，已知AB的长度x=4m，a与AB间的动摩擦因数μ1 = 0.25， b 与 BC 间的动摩擦因数μ2=0.5，取 g=10m/s2， sin37°=0.6， cos37° = 0.8， 求

(1)滑块a到达B点时的速度大小；

(2)斜面上P、C间的距离。

Answer 1

【答案】(1)4m/s；(2)1.24m。

【解析】

(1)滑块a从光滑圆弧轨道滑下到达B点的过程中，根据动能定理有：

代入数据解得

v＝4m/s

(2)滑块a到达B点后做平抛运动，根据平抛运动的规律有：

x′＝vt，y＝，tanθ=

代入数据解得

t＝0.6s

滑块b从斜面底端上滑时，根据牛顿第二定律有：

mgsinθ+μ2mgcosθ＝ma1

代入数据解得

a1＝10m/s2

向上运动的时间

t1=＜0.6s

然后接着下滑，根据牛顿第二定律有：

mgsinθ﹣μ2mgcosθ＝ma2

代入数据得

a2＝2m/s2

可得P、C间的距离

x=

代入数据解得

x＝1.24m