题目内容
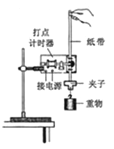
【题目】如图所示装置,可以进行以下实验:
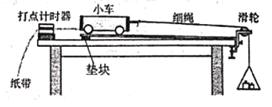
A.“研究匀变速直线运动”
B.“验证牛顿第二定律”
C.“研究合外力做功和物体动能变化关系
(1)在 A、B、C 这三个实验中,_____需要平衡摩擦阻 力。
(2)已知小车的质量为 M,盘和砝码的总质量为m,且将 mg 视为细绳对小车的拉力;为此需要满足 m![]() M。 前述 A、B、C 三个实验中,_____不需要满足此要求。
M。 前述 A、B、C 三个实验中,_____不需要满足此要求。
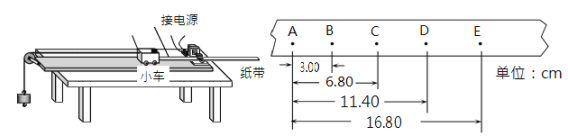
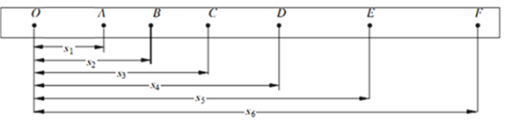
(3)接通打点计时器电源,由静止释放小车,打出若干条纸带,从中挑选一条点迹清晰的纸带,如图所 示。纸带上打出相邻两个点之间的时间间隔为T,O 点是打点计时器打出的第一个点,从 O 点到 A、B、C、D、E、F 点的距离依次为 s1、s2、s3、s4、s5、s6。但 OA 之间可能还有一些点没打上,打 F 点时小车已经 撞上木板末端的挡板,A 到 E 各点正常。由纸带可以求得小车加速度的表达式为_____。
(4)如果用此装置做“研究合外力做功和物体动能变化关系这个实验,由此可求得纸带上由 O 点到 D 点所对 应的运动过程中,盘和砝码受到的重力所做功的表达式 W=_____,该小车动能改变量的表达式△Ek=_____。由于实验中存在系统误差,所以W_____△Ek。(选填“小于”、“等于”或“大于”)。
(5)如果前述纸带为如图所示“用打点计时器验证机械能守恒”实验中打出的纸带, 且 OA 之间可能还有没打出的点,但 A 到 F 各点都正常,有两位同学提出了处理数据的办法,其中合理的是:_____
甲:如果 BC-AB=CD-BC=DE-CD=EF-DE,则重锤机械能守恒;乙:以各点对应的x为横坐标,以各点速度平方 v2 为纵坐标,描点作图线,若图线为直线,且斜率为 2g,则重锤机械能守恒.
【答案】(1)BC (2)A(3)![]() (4)mgs4;
(4)mgs4;![]() ;大于;(5)乙
;大于;(5)乙
【解析】
(1)在 A、B、C 这三个实验中,“验证牛顿第二定律”、“研究合外力做功和物体动能变化关系,都需要平衡摩擦阻力;故选BC。
(2)已知小车的质量为 M,盘和砝码的总质量为 m,且将 mg 视为细绳对小车的拉力。为此需要满足 m![]() M。 前述 A、B、C 三个实验中,实验A只需要小车做匀加速运动即可,不需要满足此要求。
M。 前述 A、B、C 三个实验中,实验A只需要小车做匀加速运动即可,不需要满足此要求。
(3)由题意可知,求解小车的加速度可用从A到E之间的纸带来求解,则根据x=aT2可得![]()
(4)纸带上由O点到D点所对应的运动过程中,盘和砝码受到的重力所做功的表达式:W=mgs4;打D点时的速度:![]() ,
,
则小车动能的改变量:![]() ;
;
由于实验中存在系统误差,所以盘和砝码受到的重力所做功W大于小车动能的增量△Ek。
(5)如果 BC-AB=CD-BC=DE-CD=EF-DE,则重物做匀加速下落,但是不能说明加速度就等于g,则不能说明重锤机械能守恒,故甲错误;以各点对应的x为横坐标,以各点速度平方v2为纵坐标,描点作图线,若图线为直线,且斜率为 2g,则满足v2=2gx,重物下落的加速度为g,则重锤只有重力做功,机械能守恒,则乙做法正确;故选乙;

 阅读快车系列答案
阅读快车系列答案