题目内容
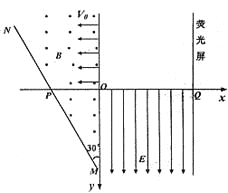
【题目】如图所示，真空中四个相同的矩形匀强磁场区域，高为4d，宽为d，中间两个磁场区域间隔为2d，中轴线与磁场区域两侧相交于O、O′点，各区域磁感应强度大小相等．某粒子质量为m、电荷量为+q，从O沿轴线射入磁场．当入射速度为v0时，粒子从O上方
处射出磁场．取sin53°=0.8，cos53°=0.6．
（1）求磁感应强度大小B；
（2）入射速度为5v0时，求粒子从O运动到O′的时间t；
（3）入射速度仍为5v0，通过沿轴线OO′平移中间两个磁场（磁场不重叠），可使粒子从O运动到O′的时间增加Δt，求Δt的最大值．
【答案】（1）
（2）
（3）
【解析】（1）粒子圆周运动的半径
由题意知
，解得
（2）设粒子在矩形磁场中的偏转角为α
由d=rsinα，得sinα=
，即α=53°
在一个矩形磁场中的运动时间
，解得
直线运动的时间
，解得
则
（3）将中间两磁场分别向中央移动距离x
粒子向上的偏移量y=2r（1–cosα）+xtanα
由y≤2d，解得
则当xm= 
时，Δt有最大值
粒子直线运动路程的最大值
增加路程的最大值
增加时间的最大值
练习册系列答案
名校课堂系列答案
相关题目
