��Ŀ����
����Ŀ����ͼ��ʾ��ˮƽ��������һ������m=1kg��С��飬С���ֱ���ˮƽ���õ����ʵ��ɺͲ����쳤������ϸ��һ�����������ɵľ���ϵ��K=100N/m��С����ˮƽ����䶯Ħ��������=0.2����ϸ������ֱ�������=45O��ʱС��鴦�ھ�ֹ״̬�������������ѹ����ʱ����ϸ�ߣ�����һ��ʱ��tС���������ܡ�g=10m/s2����
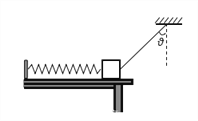
��1��ϸ�߱�����ǰ���ܵ�������
��2������ϸ��˲��С���ļ��ٶȣ�
��3��t���ʱ������Ħ�����������ܡ�
���𰸡�(1)![]() ��2��
��2��![]() ����ˮƽ���� ��3��
����ˮƽ���� ��3��![]()
��������(1) ϸ����ǰ�����壬������ƽ����![]()
���![]() N ��
N ��
��2������ϸ��˲�䣬�����壬��ţ�ٵڶ����ɵã�
![]()
![]()
![]()
���![]() m/s2������ˮƽ������
m/s2������ˮƽ������
��3����![]() ʱ������Ķ��������
ʱ������Ķ��������
![]() m
m
��![]() ���
���![]() m
m
Ħ��������Ϊ![]() J��
J��

��ϰ��ϵ�д�
 ��ĩ�óɼ�ϵ�д�
��ĩ�óɼ�ϵ�д� 99��1������ĩ��ѵ��ϵ�д�
99��1������ĩ��ѵ��ϵ�д� ��ǿ��У��ĩ���100��ϵ�д�
��ǿ��У��ĩ���100��ϵ�д� �óɼ�1��1��ĩ���100��ϵ�д�
�óɼ�1��1��ĩ���100��ϵ�д� ��״Ԫ���źþ�ϵ�д�
��״Ԫ���źþ�ϵ�д�
�����Ŀ