题目内容

如图,一无限长光滑斜面的底端静置一个物体,从某时刻开始有一个沿斜面向上的恒力F作用在物体上,使物体沿斜面向上滑去.经过时间t突然撤去该力,又经过相同的时间t物体返回斜面的底部.在物体加速沿斜面上滑的过程中,F的平均功率为
,重力的平均功率为
.在物体运动的整个过程中,F的瞬时功率的最大值为P
1,重力的瞬时功率的最大值为P
2.则有
( )
| |
| |
分析:瞬时功率表达式为P=Fv,平均功率表达式为
=F
=
,选择公式进行解决.此外,物体先加速后减速到零再反向加速运动到斜面底部,求解出瞬时速度和平均速度是关键
解答:解:设向上加速阶段加速度大小为a
1,加速度向下时大小为a
2,斜面倾角为θ,则有:
F-mgsinθ=ma
1①
mgsinθ=ma
2②
设向上加速的位移为s,则:
s=
a
1t
2③
-s=a
1t×t-
a2t2④
解①②③④得:a
2=3a
1F=
mgsinθ
设力F撤掉时的速度为v,物块到达斜面低端是的速度为v′,则:
v=a
1t
v′=a
2t-a
1t=2a
1t=2v
故:p
1=Fv
p
2=mgsinθv′=
F×2v=
Fv故:p
1:p
2=2:3
故D正确
=F×
=
Fv=mgsinθ×
=
mgsinθv故
:=4:3
故A正确
故选AD
点评:分析好物体的运动情景,求出最大功率对应的位置或状态,正确选择公式是解决本题的关键
练习册系列答案
相关题目
 如图,一无限长光滑斜面的底端静置一个物体,从某时刻开始有一个沿斜面向上的恒力F作用在物体上,使物体沿斜面向上滑去.经过时间t突然撤去该力,又经过相同的时间t物体返回斜面的底部.在物体加速沿斜面上滑的过程中,F的平均功率为
如图,一无限长光滑斜面的底端静置一个物体,从某时刻开始有一个沿斜面向上的恒力F作用在物体上,使物体沿斜面向上滑去.经过时间t突然撤去该力,又经过相同的时间t物体返回斜面的底部.在物体加速沿斜面上滑的过程中,F的平均功率为
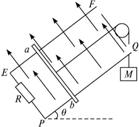
 如图所示,无限长金属导轨EF、PQ固定在倾角为θ=53°的光滑绝缘斜面上,轨道间距L=1m,底部接入一阻值为R=0.4Ω的定值电阻,上端开口.垂直斜面向上的匀强磁场的磁感应强度B=2T.一质量为m=0.5kg的金属棒ab与导轨接触良好,ab与导轨间动摩擦因数μ=0.2,ab连入导轨间的电阻r=0.1Ω,电路中其余电阻不计.现用一质量为M=2.86kg的物体通过一不可伸长的轻质细绳绕过光滑的定滑轮与ab相连.由静止释放M,不计空气阻力,当M下落高度h=2.0m时,ab开始匀速运动(运动中ab始终垂直导轨,并接触良好).
如图所示,无限长金属导轨EF、PQ固定在倾角为θ=53°的光滑绝缘斜面上,轨道间距L=1m,底部接入一阻值为R=0.4Ω的定值电阻,上端开口.垂直斜面向上的匀强磁场的磁感应强度B=2T.一质量为m=0.5kg的金属棒ab与导轨接触良好,ab与导轨间动摩擦因数μ=0.2,ab连入导轨间的电阻r=0.1Ω,电路中其余电阻不计.现用一质量为M=2.86kg的物体通过一不可伸长的轻质细绳绕过光滑的定滑轮与ab相连.由静止释放M,不计空气阻力,当M下落高度h=2.0m时,ab开始匀速运动(运动中ab始终垂直导轨,并接触良好).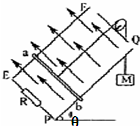 如图所示,无限长金属导轨EF、PQ固定在倾角为θ=30°的光滑绝缘斜面上,轨道间距L=1m,底部接入一阻值为R=0.4Ω的定值电阻,上端开口.垂直斜面向上的匀强磁场的磁感应强度B=2T.一质量为m=0.8kg的金属棒ab与导轨接触良好,ab与导轨间没有摩擦,ab连入导轨间的电阻r=0.1Ω,电路中其余电阻不计.现用一质量为M=2kg的物体通过一不可伸长的轻质细绳绕过光滑的定滑轮与ab相连.由静止释放M,不计空气阻力,当M下落高度h=2.0m时,ab开始匀速运动(运动中ab始终垂直导轨,并接触良好,g=10m/s2).求:
如图所示,无限长金属导轨EF、PQ固定在倾角为θ=30°的光滑绝缘斜面上,轨道间距L=1m,底部接入一阻值为R=0.4Ω的定值电阻,上端开口.垂直斜面向上的匀强磁场的磁感应强度B=2T.一质量为m=0.8kg的金属棒ab与导轨接触良好,ab与导轨间没有摩擦,ab连入导轨间的电阻r=0.1Ω,电路中其余电阻不计.现用一质量为M=2kg的物体通过一不可伸长的轻质细绳绕过光滑的定滑轮与ab相连.由静止释放M,不计空气阻力,当M下落高度h=2.0m时,ab开始匀速运动(运动中ab始终垂直导轨,并接触良好,g=10m/s2).求: