题目内容
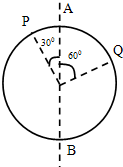
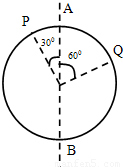
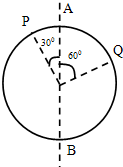如图所示为一圆环，现让圆环以它的直径AB为轴匀速转动，则环上两点P、Q的向心加速度大小之比是1：
| 3 |
1：
．| 3 |
分析：根据a=ω2r 即可求得Q点的向心加速度大小．
解答：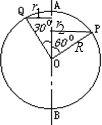
解：P、Q两点以它的直径AB为轴做匀速转动，它们的角速度相同都为ω，
所以Q点转动的半径r1=Rsin30°=
R，
P点转动的半径r2=Rsin60°=
R
根据a=ω2r 得加速度与半径成正比，
所以环上两点P、Q的向心加速度大小之比为1：
．
故答案为：1：
．
解：P、Q两点以它的直径AB为轴做匀速转动，它们的角速度相同都为ω，所以Q点转动的半径r1=Rsin30°=
| 1 |
| 2 |
P点转动的半径r2=Rsin60°=
| ||
| 2 |
根据a=ω2r 得加速度与半径成正比，
所以环上两点P、Q的向心加速度大小之比为1：
| 3 |
故答案为：1：
| 3 |
点评：该题主要考查了圆周运动基本公式的直接应用，注意同轴转动时角速度相同．
练习册系列答案
相关题目
如图所示，一圆环A套在一粗细均匀的圆木棒B上，圆环A的高度相对B的长度可以忽略不计．A和B的质量都是0.5kg，A和B之间的滑动摩擦力为3N．开始时B竖直放置，下端离地面高度h=0.8m，A在B的顶端．现让它们由静止开始自由下落，当木棒与地面相碰后，木棒以竖直向上的速度反向运动．设碰撞时间很短，碰撞无机械能损失，不考虑空气阻力，取当地的重力加速度g=10m/s2．试求：
如图所示，一圆环位于竖直平面内．圆环圆心处的一小球，OP、OQ为两根细绳，一端与球相连另一端固定在圆环上．OP呈水平，OQ与竖直方向成30°角．现保持小球位置不动，将圆环沿顺时针方向转过90°角，则在此过程中（ ）
