题目内容
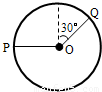
 如图所示,一圆环位于竖直平面内.圆环圆心处的一小球,OP、OQ为两根细绳,一端与球相连另一端固定在圆环上.OP呈水平,OQ与竖直方向成30°角.现保持小球位置不动,将圆环沿顺时针方向转过90°角,则在此过程中( )
如图所示,一圆环位于竖直平面内.圆环圆心处的一小球,OP、OQ为两根细绳,一端与球相连另一端固定在圆环上.OP呈水平,OQ与竖直方向成30°角.现保持小球位置不动,将圆环沿顺时针方向转过90°角,则在此过程中( )分析:将圆环沿顺时针方向转过90°角的过程中,小球的位置保持不动,受力保持平衡,由平衡条件可知,两绳拉力的合力不变,运用三角定则作出力的合成图,由正弦定理得出两绳的拉力与OP转动角度的关系,即可分析两力的变化情况.
解答:解:设小球的重力为G,圆环沿顺时针方向转过过程中OP与竖直方向的夹角α时,OP和OQ的拉力大小分别为T1、T2.由题,小球的位置保持不动,受力保持平衡,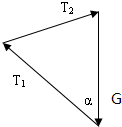 由平衡条件可知,两绳拉力的合力不变,运用三角定则作出力的合成图,如图,小球受到的重力G和T1、T2组成一个闭合的三角形.由几何知识得知,T1、T2的夹角保持60°,由正弦定理得
由平衡条件可知,两绳拉力的合力不变,运用三角定则作出力的合成图,如图,小球受到的重力G和T1、T2组成一个闭合的三角形.由几何知识得知,T1、T2的夹角保持60°,由正弦定理得
=
=
得,T1=
,T2=
在α从90°转到0°的过程中,根据数学知识得知,sin(120°-α)先增大后减小,而sinα减小,所以OP绳所受拉力先增大后减小,OQ绳所受拉力一直减小.
故选B
 由平衡条件可知,两绳拉力的合力不变,运用三角定则作出力的合成图,如图,小球受到的重力G和T1、T2组成一个闭合的三角形.由几何知识得知,T1、T2的夹角保持60°,由正弦定理得
由平衡条件可知,两绳拉力的合力不变,运用三角定则作出力的合成图,如图,小球受到的重力G和T1、T2组成一个闭合的三角形.由几何知识得知,T1、T2的夹角保持60°,由正弦定理得| T1 |
| sin(180°-60°-α) |
| T2 |
| sinα |
| G |
| sin60° |
得,T1=
| Gsin(120°-α) |
| sin60° |
| Gsinα |
| sin60° |
在α从90°转到0°的过程中,根据数学知识得知,sin(120°-α)先增大后减小,而sinα减小,所以OP绳所受拉力先增大后减小,OQ绳所受拉力一直减小.
故选B
点评:本题的解题关键是运用数学知识得到两绳拉力的表达式,考查运用数学工具处理物理问题的能力,同时,本题用三角形定则作图比较简单.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
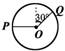
 如图所示,一圆环位于竖直平面内.圆环圆心处的一小球,OP、OQ为两根细绳,一端与球相连另一端固定在圆环上.OP呈水平,OQ与竖直方向成30°角.现保持小球位置不动,将圆环沿顺时针方向转过90°角,则在此过程中
如图所示,一圆环位于竖直平面内.圆环圆心处的一小球,OP、OQ为两根细绳,一端与球相连另一端固定在圆环上.OP呈水平,OQ与竖直方向成30°角.现保持小球位置不动,将圆环沿顺时针方向转过90°角,则在此过程中