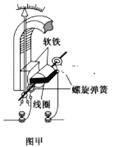
题目内容
【题目】导线中自由电子的定向移动形成电流,电流可以从宏观和微观两个角度来认识。
(1)一段通电直导线的横截面积为S,它的摩尔质量为M,密度为ρ,阿伏伽德罗常数位NA。导线中每个带电粒子定向运动的速率为υ,粒子的电荷量为e,假设每个电子只提供一个自由电子。
①推导该导线中电流的表达式;
②如图所示,电荷定向运动时所受洛伦兹力的矢量和,在宏观上表现为导线所受的安培力。按照这个思路,请你尝试由安培力的表达式推导出洛伦兹力的表达式。
(2)经典物理学认为金属导体中恒定电场形成稳恒电流。金属导体中的自由电子在电场力的作用下,定向运动形成电流。自由电子在定向运动的过程中,不断地与金属离子发生碰撞。碰撞后自由电子定向运动的速度变为零,将能量转移给金属离子,使得金属离子的热运动更加剧烈,这就是焦耳热产生原因。
某金属直导线电阻为R,通过的电流为I。请从宏观和微观相结合的角度,证明:在时间t内导线中产生的焦耳热为Q=I2Rt(可设电子与离子两次碰撞的时间间隔t0,碰撞时间忽略不计,其余需要的物理量可自设)。

【答案】(1)①![]() ②见解析(2)见解析
②见解析(2)见解析
【解析】
(1)①金属导线单位体积内电子个数
![]()
在时间t内流过导线横截面的带电粒子数
N=![]()
通过导线横截面的总电荷量
Q=Ne
导线中电流
I=![]()
联立以上三式可以推导出
I=![]()
②导线受安培力大小
F安=BIL。
长L的导线内总的带电粒子数
N=nSL![]()
又
I=![]()
![]()
电荷定向运动时所受洛伦兹力的矢量和,表现为导线所受的安培力,即
Nf=F安
联立以上三式可以推导出洛伦兹力的表达式
f=evB
(2)方法1:
设金属导体长为L,横截面积为S,两端电压为U,导线中的电场强度
E=![]()
设金属导体中单位体积中的自由电子数为n,则金属导体中自由电子总数
![]()
设自由电子的带电量为e,连续两次碰撞时间间隔为t0,定向移动的平均速度为υ,则一次碰撞的能量转移
![]()
一个自由电子在时间t内与金属离子碰撞次数为![]()
金属导体中在时间t内全部自由电子与金属离子碰撞,产生的焦耳热
![]()
又
![]() U=IR
U=IR
联立解以上各式推导得
![]()
方法2:
设金属导体长为L,横截面积为S,两端电压为U,导线中的电场强度
E=![]()
设金属导体中单位体积中的自由电子数为n,则金属导体中自由电子数
![]()
在纯电阻电路中,电流做的功等于焦耳热,即Q=W
电流做的功等于电功率乘时间
W=Pt
电功率等于电场力对长为L的导线中所有带电粒子做功功率的总和
![]()
自由电子受的电场力
F=Ee
又
![]() U=IR
U=IR
联立解以上各式推导得
![]()

 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案【题目】在测量电阻的实验中,提供的器材有:3V稳压电源E、滑动变阻器R、电压表V、电流表A、待测电阻Rx,以及开关S、导线等。
实验要求:
①电流表内接;②调节滑线变阻器可使电压表的示数在0~3V间变化.
(1)在实验中,有的同学连成如图所示的电路,其中a,b,c,…,k是表示接线柱的字母.请将图中接线错误(用导线两端接线柱的字母表示)、引起的后果、改正的方法(用“改接”、“撤销”或“增添”等词语描述),分别填在相应的表格中________________________。
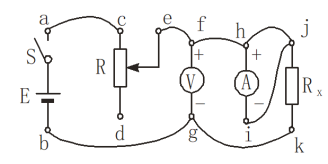
接线错误 | 引起的后果 | 改正的方法 |
(2)实验中所用电压表的内阻约为20kΩ,电流表的内阻约为10Ω,按正确的电路操作,读得的各组数据用+标于坐标图上,如图所示.根据各点表示的数据描出I-U图线________,由此求得该电阻的阻值Rx=_____________Ω。
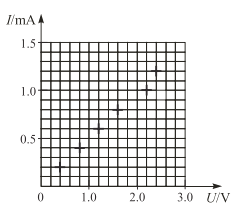
(3)本实验中电阻的测量值比真实值偏___________(填“大”或“小”),其原因是___________。