题目内容
15.上星期五运动会,甲、乙两同学在直跑道上练习“4×100m”接力,他们在奔跑时有相同的最大速度,乙从静止开始全力奔跑需跑出25m才能达到最大速度,这一过程可看做匀变速运动.现在甲持棒以最大速度向乙奔来,乙在接力区待机全力奔出.(1)若要求乙接棒时的速度达到最大速度的80%,则乙在接力区须奔出多少距离?乙应在距离甲多远处起跑?
(2)若最大速度为v=10m/s,在甲距离乙x0=6m时,乙才全力奔出,甲在乙奔出时立即改为以a1=1m/s2的加速度做匀减速直线运动,直到速度减到零为止,则此过程中经过多长时间甲、乙相遇?
分析 (1)根据初速度为0的匀变速直线运动速度位移公式v2=2ax,求出乙在接力区需奔出的距离.根据平均速度公式求出乙加速至交接棒所经过的位移${x}_{2}=\frac{0+{v}_{2}}{2}t=0.4{v}_{1}t=16m$,而甲在这段时间内的位移x甲=v1t,两人位移之差即为乙距离甲的起跑距离;
(2)根据匀变速直线运动位移速度公式求出乙的加速度,再根据甲乙相遇时位移关系列式求解.
解答 解:(1)乙起跑后做初速度为0的匀加速直线运动,设最大速度为v1,x1为达到最大速度经历的位移,v2为乙接棒时的速度,x2为接棒时经历的位移,有:
v12=2ax1
v22=2ax2
v2=v1×80%
得:x2=0.64,x1=16m
故乙在接力需奔出的距离为16m.
设乙加速至交接棒的时间为t,
${x}_{2}=\frac{0+{v}_{2}}{2}t=0.4{v}_{1}t=16m$
x甲=v1t
△x=x甲-x2=0.6v1t=24m.
故乙应在距离甲24m处起跑.
(2)乙的加速度${a}_{2}=\frac{{v}^{2}}{2x}=\frac{100}{2×25}=2m/{s}^{2}$,设经过时间t,甲乙相遇,则有:
$vt-\frac{1}{2}{a}_{1}{t}^{2}=\frac{1}{2}{a}_{2}{t}^{2}+{x}_{0}$
解得:t=6s
答:(1)乙在接力区须奔出16m的距离,乙应在距离甲24m处起跑;
(2)此过程中经过6s时间甲、乙相遇.
点评 解决本题的关键掌握初速度为0的匀变速直线运动的速度位移公式v2=2ax.以及知道乙距离甲的起跑距离等于在乙起跑到接棒这段时间内两人的位移之差.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
5.下列情况可能出现的是( )
| A. | 物体运动的速度很小,加速度却很大 | |
| B. | 物体运动的速度很大,加速度却很小 | |
| C. | 物体运动的速度不变,加速度却在变化 | |
| D. | 物体运动的速度在变化,加速度却不变 |
3.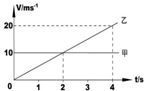 水平地面上两个质点甲和乙,同时由同一地点沿同一方向作直线运动,它们的v-t图线如图所示.下列判断正确的是( )
水平地面上两个质点甲和乙,同时由同一地点沿同一方向作直线运动,它们的v-t图线如图所示.下列判断正确的是( )
 水平地面上两个质点甲和乙,同时由同一地点沿同一方向作直线运动,它们的v-t图线如图所示.下列判断正确的是( )
水平地面上两个质点甲和乙,同时由同一地点沿同一方向作直线运动,它们的v-t图线如图所示.下列判断正确的是( )| A. | 前4s内,甲的平均速度等于乙的平均速度 | |
| B. | 4秒末甲和乙相遇 | |
| C. | 前2秒甲在前,后2秒乙在前 | |
| D. | 甲做匀速直线运动,乙做匀加速直线运动 |
10. 小文同学在探究物体做曲线运动的条件时,将一条形磁铁放在桌面的A位置,让小钢珠在水平桌面上以初速度v0运动,得到小钢珠的运动轨迹.图中a、b、c、d哪一条为其运动轨迹( )
小文同学在探究物体做曲线运动的条件时,将一条形磁铁放在桌面的A位置,让小钢珠在水平桌面上以初速度v0运动,得到小钢珠的运动轨迹.图中a、b、c、d哪一条为其运动轨迹( )
 小文同学在探究物体做曲线运动的条件时,将一条形磁铁放在桌面的A位置,让小钢珠在水平桌面上以初速度v0运动,得到小钢珠的运动轨迹.图中a、b、c、d哪一条为其运动轨迹( )
小文同学在探究物体做曲线运动的条件时,将一条形磁铁放在桌面的A位置,让小钢珠在水平桌面上以初速度v0运动,得到小钢珠的运动轨迹.图中a、b、c、d哪一条为其运动轨迹( )| A. | a | B. | b | C. | c | D. | d |
20.关于质点,下列说法中正确的是( )
| A. | 质点是真实存在的用来代替物体的有质量的点 | |
| B. | 很小的物体总可以看成质点,较大的物体有时也能看成质点 | |
| C. | 研究地球公转的周期时,可以把地球看成质点 | |
| D. | 研究子弹穿过薄纸的时间时,可以把子弹看成质点 |
7.伽利略开创了实验研究和逻辑推理相结合探索自然规律的科学方法,利用这种方法伽利略发现的规律有( )
| A. | 物体之间普遍存在相互吸引力 | |
| B. | 力不是维持物体运动的原因 | |
| C. | 物体间的相互作用力总是大小相等、方向相反 | |
| D. | 忽略空气阻力,重物与轻物下落得同样快 |
4.在物理学发展中,许多物理学家的科学研究推动了人类文明进程.对以下几位物理学家所做贡献的叙述中,符合史实的是( )
| A. | 卡文迪许发现了万有引力定律 | |
| B. | 亚里士多德通过理想实验提出力并不是维持物体运动的原因 | |
| C. | 库仑总结并确认了真空中两个静止点电荷之间的相互作用规律 | |
| D. | 牛顿应用“理想斜面实验”推翻了亚里士多德的“力是维持物体运动的原因”观点 |