题目内容
5.如图1所示,为“探究加速度与力、质量的关系”实验装置及数字化信息系统获得了小车加速度a与钩码的质量及小车和砝码的质量对应关系图.钩码的质量为m1,小车和砝码的质量为m2,重力加速度为g.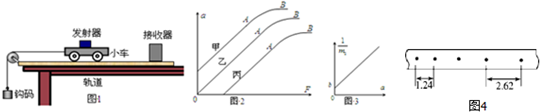
(1)下列说法正确的是D.
A.每次在小车上加减砝码时,应重新平衡摩擦力
B.实验时若用打点计时器应先释放小车后接通电源
C.本实验m2应远小于m1
D.在用图象探究加速度与质量关系时,应作a-$\frac{1}{{m}_{2}}$图象
(2)实验时,某同学由于疏忽,遗漏了平衡摩擦力这一步骤,测得F=m1g,作出a-F图象,他可能作出图2中丙 (选填“甲”、“乙”、“丙”)图线.此图线的AB段明显偏离直线,造成此误差的主要原因是C.
A.小车与轨道之间存在摩擦 B.导轨保持了水平状态
C.砝码盘和砝码的总质量太大 D.所用小车的质量太大
(3)实验时,某同学遗漏了平衡摩擦力这一步骤,若轨道水平,他测量得到的$\frac{1}{{m}_{2}}$-a图象如图3.设图中直线的斜率为k,在纵轴上的截距为b,则小车与木板间的动摩擦因数μ$\frac{b}{gk}$,钩码的质量m1=$\frac{1}{gk}$.
(4)实验中打出的纸带如图4所示.相邻计数点间的时间是0.1s,图中长度单位是cm,由此可以算出小车运动的加速度是0.46m/s2.(保留两位有效数字)
分析 如果没有平衡摩擦力的话,就会出现当有拉力时,物体不动的情况.得出图象弯曲的原因是:未满足沙和沙桶质量远小于小车的质量.
根据牛顿第二定律,列出小车的滑动摩擦力大小,然后结合图象的斜率与截距,可以得出结论.
解答 解:(1)A、每次在小车上加减砝码时,不需要重新平衡摩擦力,故A错误.
B、实验时应先接通电源,再释放纸带,故B错误.
C、为了使钩码的重力表示绳子的拉力,应满足m1应远小于m2,故C错误.
D、在用图象探究加速度与质量关系时,若作a-m图线,图线为曲线,无法得出a与m的定量关系,所以应作a-$\frac{1}{{m}_{2}}$图象,故D正确.
(2)漏了平衡摩擦力这一步骤,就会出现当有拉力时,物体不动的情况.故图线为丙.
当不满足m1<<m2时,随m1的增大物体的加速度a逐渐减小,故图象弯曲的原因是:所挂钩码的总质量太大,不满足沙和沙桶质量远小于小车的质量.故选:C.
(3)根据牛顿第二定律可知,m1g-μm2g=m2a;
结合$\frac{1}{{m}_{2}}$-a图象,可得:$\frac{1}{{m}_{2}}=\frac{μ}{{m}_{1}}+\frac{1}{{m}_{1}g}a$,
设图中直线的斜率为k,在纵轴上的截距为b,因此钩码的质量m1=$\frac{1}{gk}$,小车与木板间的动摩擦因数μ=$\frac{b}{gk}$.
(4)根据${x}_{4}-{x}_{1}=3a{T}^{2}$得,加速度a=$\frac{{x}_{4}-{x}_{1}}{3{T}^{2}}=\frac{(2.62-1.24)×1{0}^{-2}}{3×0.01}$=0.46m/s2.
故答案为:(1)D(2)丙、C(3)$\frac{b}{gk}$,$\frac{1}{gk}$,(4)0.46m/s2;
点评 会根据实验原理分析分析为什么要平衡摩擦力和让小车的质量M远远大于小桶(及砝码)的质量m,对于图象问题,关键得出两个物理量之间的关系,结合图线的斜率和截距进行求解.

 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案 如图所示,一带有四分之一光滑圆弧滑道的木块放置在粗糙的水平面上,圆弧滑道的圆心为O点,OA和OB分别为水平半径和竖直半径.现让一质量为m的小滑块从A点由静止释放(木块始终静止).空气阻力不计,重力加速度为g.在小滑块A点下滑到B点的过程中,地面对木块的最大静摩擦力为( )
如图所示,一带有四分之一光滑圆弧滑道的木块放置在粗糙的水平面上,圆弧滑道的圆心为O点,OA和OB分别为水平半径和竖直半径.现让一质量为m的小滑块从A点由静止释放(木块始终静止).空气阻力不计,重力加速度为g.在小滑块A点下滑到B点的过程中,地面对木块的最大静摩擦力为( )| A. | $\frac{mg}{2}$ | B. | mg | C. | $\frac{3mg}{2}$ | D. | 2mg |
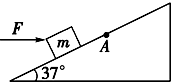 一个质量m=0.5kg的滑块在倾角为θ=37°的足够长的固定斜面上,受到一个大小为10N的水平推力F作用,以v0=10m/s的速度沿斜面匀速上滑.(sin37°=0.6,cos37°=0.8取g=10m/s2)
一个质量m=0.5kg的滑块在倾角为θ=37°的足够长的固定斜面上,受到一个大小为10N的水平推力F作用,以v0=10m/s的速度沿斜面匀速上滑.(sin37°=0.6,cos37°=0.8取g=10m/s2)
 如图所示,两根正对的平行金属直轨道MN、M′N′位于同一水平面上,两轨道之间的距离l=0.50m.轨道的M、M′之间有一阻值R=0.50Ω的定值电阻,NN′端与两条位于竖直面内的半圆形光滑金属轨道NP、N′P′平滑连接,两半圆轨道的半径均为R0=0.50m.直轨道的右端处于竖直向下、磁感应强度B=0.60T的匀强磁场中,磁场区域的宽度d=0.80m,且其右边界与NN′重合.现有一质量m=0.20kg、电阻r=0.10Ω恰好能放在轨道上的导体杆ab静止在距磁场的左边界s=2.0m处.在与杆垂直的水平恒力F=2.0N的作用下ab杆开始运动,当运动至磁场的左边界时撤去F,导体杆ab穿过磁场区域后,沿半圆形轨道运动,结果恰好通过半圆形轨道的最高点PP′.已知导体杆ab在运动过程中与轨道接触良好,且始终与轨道垂直,导体杆ab与直轨道之间的动摩擦因数μ=0.10,轨道的电阻可忽略不计,g取10m/s2.求:
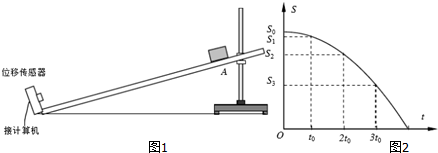
如图所示,两根正对的平行金属直轨道MN、M′N′位于同一水平面上,两轨道之间的距离l=0.50m.轨道的M、M′之间有一阻值R=0.50Ω的定值电阻,NN′端与两条位于竖直面内的半圆形光滑金属轨道NP、N′P′平滑连接,两半圆轨道的半径均为R0=0.50m.直轨道的右端处于竖直向下、磁感应强度B=0.60T的匀强磁场中,磁场区域的宽度d=0.80m,且其右边界与NN′重合.现有一质量m=0.20kg、电阻r=0.10Ω恰好能放在轨道上的导体杆ab静止在距磁场的左边界s=2.0m处.在与杆垂直的水平恒力F=2.0N的作用下ab杆开始运动,当运动至磁场的左边界时撤去F,导体杆ab穿过磁场区域后,沿半圆形轨道运动,结果恰好通过半圆形轨道的最高点PP′.已知导体杆ab在运动过程中与轨道接触良好,且始终与轨道垂直,导体杆ab与直轨道之间的动摩擦因数μ=0.10,轨道的电阻可忽略不计,g取10m/s2.求: 屋檐上每隔相同的时间间隔滴下一滴水,当第5滴正欲滴下时,第1滴已刚好到达地面,而第3滴与第2滴分别位于高为1m的窗户的上、下沿,如图所示,问:
屋檐上每隔相同的时间间隔滴下一滴水,当第5滴正欲滴下时,第1滴已刚好到达地面,而第3滴与第2滴分别位于高为1m的窗户的上、下沿,如图所示,问: 如图所示的空间分为Ⅰ、Ⅱ、Ⅲ三个区域,各边界面相互平行,Ⅰ区域存在匀强电场,电场强度E=1.0×104V/m,方向垂直边界面向右,Ⅱ、Ⅲ区域存在匀强磁场,磁场的方向分别为垂直纸面向外和垂直纸面向里,磁感应强度分别为B1=2B2=2.0T.三个区域宽度分别为d1=5.0m、d2=2.5m,d3=5.0m,一质量m=1.6×10-9kg、电荷量q=+1.6×10-6C的粒子从O点由静止释放,粒子的重力忽略不计.求:
如图所示的空间分为Ⅰ、Ⅱ、Ⅲ三个区域,各边界面相互平行,Ⅰ区域存在匀强电场,电场强度E=1.0×104V/m,方向垂直边界面向右,Ⅱ、Ⅲ区域存在匀强磁场,磁场的方向分别为垂直纸面向外和垂直纸面向里,磁感应强度分别为B1=2B2=2.0T.三个区域宽度分别为d1=5.0m、d2=2.5m,d3=5.0m,一质量m=1.6×10-9kg、电荷量q=+1.6×10-6C的粒子从O点由静止释放,粒子的重力忽略不计.求: