题目内容
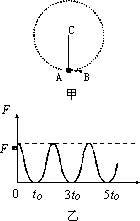
图甲所示为一根竖直悬挂的不可伸长的轻绳,下端拴一小物块A,上端固定在C点且与一能测量绳的拉力的测力传感器相连.已知有一质量为m0的子弹B沿水平方向以速度v0射入A内(未穿透),接着两者一起绕C点在竖直面内做圆周运动,在各种阻力都可忽略的条件下测力传感器测得绳的拉力F随时间![]() 的变化关系如图乙所示.已知子弹射入的时间极短,且图乙中t=0为A、B开始以相同速度运动的时刻,根据力学规律和题中(包括图)提供的信息,对反映悬挂系统本身性质的物理量(例如A的质量)及A、B一起运动过程中的守恒量,你能求得哪些定量的结果?
的变化关系如图乙所示.已知子弹射入的时间极短,且图乙中t=0为A、B开始以相同速度运动的时刻,根据力学规律和题中(包括图)提供的信息,对反映悬挂系统本身性质的物理量(例如A的质量)及A、B一起运动过程中的守恒量,你能求得哪些定量的结果?
答案:
解析:
解析:
|
由图乙可直接看出,A、B一起做周期性运动,运动的周期T=2t0① 令 m0v0=(m0+m)v1② 在最低点和最高点处运用牛顿定律可得
由图乙可知,F2=0⑥F1=Fm⑦由以上各式可解得,反映系统性质的物理量是
A、B一起运动过程中的守恒量是机械能E,若以最低点为势能的零点,则
|

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
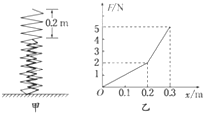 在现代汽车技术中,一般轿车都设置有“汽车悬架”,麦弗逊式及烛式悬架都是将螺旋弹簧和减振器有机组合,对缓冲冲击和消减冲击产生的振动全面考虑,大大提高了乘坐者的舒适性.现在有一组合弹簧,一根大弹簧内套了一根小弹簧,大弹簧比小弹簧长0.2m.为了测量弹簧的劲度系数,把组合弹簧的一端平齐并竖直固定,另一端处于自由状态,如图甲所示.当压缩此组合弹簧时,测得力与压缩距离之间的关系图线如图乙所示,则大弹簧的劲度系数k1和小弹簧的劲度系数k2分别为多少?
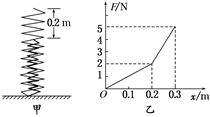
在现代汽车技术中,一般轿车都设置有“汽车悬架”,麦弗逊式及烛式悬架都是将螺旋弹簧和减振器有机组合,对缓冲冲击和消减冲击产生的振动全面考虑,大大提高了乘坐者的舒适性.现在有一组合弹簧,一根大弹簧内套了一根小弹簧,大弹簧比小弹簧长0.2m.为了测量弹簧的劲度系数,把组合弹簧的一端平齐并竖直固定,另一端处于自由状态,如图甲所示.当压缩此组合弹簧时,测得力与压缩距离之间的关系图线如图乙所示,则大弹簧的劲度系数k1和小弹簧的劲度系数k2分别为多少?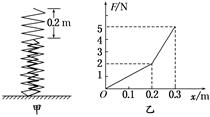


















 g
g
 。
。





