题目内容
10. 如图所示,质量为m的小球A穿在绝缘细杆上,杆的倾角为α,小球A带正电,电量为q,在杆上B点处固定一个电量为Q的正电荷.将A由距B竖直高度为H处无初速释放,小球A下滑过程中电量不变.不计A与细杆间的摩擦,整个装置处在真空中.已知静电力恒量k和重力加速度g,求:
如图所示,质量为m的小球A穿在绝缘细杆上,杆的倾角为α,小球A带正电,电量为q,在杆上B点处固定一个电量为Q的正电荷.将A由距B竖直高度为H处无初速释放,小球A下滑过程中电量不变.不计A与细杆间的摩擦,整个装置处在真空中.已知静电力恒量k和重力加速度g,求:(1)A球刚释放时的加速度;
(2)当A球的速度最大时,求此时的库仑力多大.
(3)当A球的速度最大时,求此时A球与B点的距离.
分析 (1)对A球受力分析,受到重力、支持力和静电斥力,根据牛顿第二定律求加速度;
(2)小球A先加速下滑,当静电斥力等于重力的下滑分量时,小球速度最大,求的库仑力
(3)球A先加速下滑,当静电斥力等于重力的下滑分量时,小球速度最大,求的库仑力
解答 解:(1)由牛顿第二定律得:mgsinα-F=ma,
由库仑定律得:F=k$\frac{Qq}{{r}^{2}}$,由几何知识得:r=$\frac{H}{sinα}$,
解得:a=gsinα-$\frac{kQqsi{n}^{2}α}{m{H}^{2}}$;
(2)当A球所受合力为零,加速度为零时,速度最大,即F=mgsinα
(3)当A球所受合力为零,加速度为零时,速度最大.
设此时AB间距离为L,由平衡条件得:mgsinα=k$\frac{Qq}{{r}^{2}}$,
解得:$L=\sqrt{\frac{kQq}{mgsinα}}$;
答:(1)A球刚释放时的加速度为gsinα-$\frac{kQqsi{n}^{2}α}{m{H}^{2}}$;
(2)当A球的速度最大时,此时的库仑力为mgsinα
(3)当A球的速度最大时,此时A球与B点的距离为$\sqrt{\frac{kQq}{mgsinα}}$
点评 本题关键对小球A受力分析,然后根据牛顿第二定律求解加速度,根据力与速度关系分析小球A的运动情况

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
1.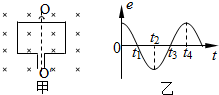 如图甲所示,矩形线圈绕轴OO′在匀强磁场中匀速转动,线圈中产生的电动势随时间变化规律如图乙所示,则( )
如图甲所示,矩形线圈绕轴OO′在匀强磁场中匀速转动,线圈中产生的电动势随时间变化规律如图乙所示,则( )
 如图甲所示,矩形线圈绕轴OO′在匀强磁场中匀速转动,线圈中产生的电动势随时间变化规律如图乙所示,则( )
如图甲所示,矩形线圈绕轴OO′在匀强磁场中匀速转动,线圈中产生的电动势随时间变化规律如图乙所示,则( )| A. | t1时刻线圈通过中性面 | B. | t2时刻线圈中磁通量最大 | ||
| C. | t3时刻线圈中磁通量变化率最大 | D. | t4时刻线圈中磁通量变化率最大 |
18.如图1所示是某同学由打点计时器得到的表示小车运动过程的一条清晰纸带,纸带上两相邻计数点间还有四个点没有画出,打点计时器打点的时间间隔T=0.02s,其中x1=7.05cm、x2=7.68cm、x3=8.33cm、x4=8.95cm、x5=9.61cm、x6=10.26cm.某同学进行实验的主要步骤是:将橡皮筋的一端固定在木板上的A

(1)如表列出了打点计时器打下B、C、F时小车的瞬时速度,请在表中填入打点计时器打下D、E两点时小车的瞬时速度.(结果保留三位有效数字)
(2)以A点为计时起点,在坐标图2中画出小车的速度-时间关系线.
(3)根据你画出的小车的速度-时间关系图线计算出小车的加速度a=0.64m/s2.

(1)如表列出了打点计时器打下B、C、F时小车的瞬时速度,请在表中填入打点计时器打下D、E两点时小车的瞬时速度.(结果保留三位有效数字)
| 位置 | B | C | D | E | F |
| 速度/(m•s-1) | 0.737 | 0.801 | 0.994 |
(3)根据你画出的小车的速度-时间关系图线计算出小车的加速度a=0.64m/s2.
15.初速度为零的α粒子、质子和一价钠离子被同一加速电场加速后垂直于电场方向进入同一偏转电场后飞离电场,则这一过程中( )
| A. | 刚从加速电场飞出的α粒子动能最大 | |
| B. | 刚从加速电场飞出的质子速度最大 | |
| C. | α粒子、质子和一价钠离子飞离偏转电场时的偏转角都相等 | |
| D. | 质子和一价钠离子从进入到飞离偏转电场过程中,动能的增量相等,且是α粒子动能增量的一半 |
2. 电流互感器是用来测量大电流的仪器,如图所示,是电流互感器使用原理示意图,以下说法正确的是( )
电流互感器是用来测量大电流的仪器,如图所示,是电流互感器使用原理示意图,以下说法正确的是( )
 电流互感器是用来测量大电流的仪器,如图所示,是电流互感器使用原理示意图,以下说法正确的是( )
电流互感器是用来测量大电流的仪器,如图所示,是电流互感器使用原理示意图,以下说法正确的是( )| A. | 因变压器将电压升高了,所以电流表示数比把电流表直接接到电路时示数大 | |
| B. | 图中电流表的示数比直接接在电路时示数小 | |
| C. | 原理图有错误,原线圈匝数应比副线圈匝数少 | |
| D. | 图中电流表的示数就是电路中的电流大小 |
19.如图所示,原来不带电的绝缘金属导体MN,有一带负电的绝缘金属球A靠近导体的M端,下列说法正确的是( )


| A. | M端带正电,N带负电 | B. | M带正电,N端不带电 | ||
| C. | M端不带电,N带负电 | D. | M端不带电,N端不带电 |
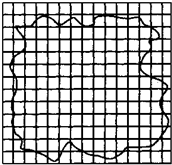 《用油膜法估测分子的大小》的实验中:
《用油膜法估测分子的大小》的实验中: 如图所示,将斜面体固定在水平面上,其两个斜面光滑,斜面上放置一质量不计的柔软薄纸带.现将质量为mA的A物体和质量为mB的B物体轻放在纸带上.两物体可视为质点,物体初始位置及数据如图所示,即在左侧斜面体上A物体距离纸带下端为1.6m,B物体放在右侧斜面体的纸带下端距离底部为3.0m.
如图所示,将斜面体固定在水平面上,其两个斜面光滑,斜面上放置一质量不计的柔软薄纸带.现将质量为mA的A物体和质量为mB的B物体轻放在纸带上.两物体可视为质点,物体初始位置及数据如图所示,即在左侧斜面体上A物体距离纸带下端为1.6m,B物体放在右侧斜面体的纸带下端距离底部为3.0m.