题目内容
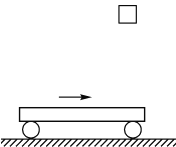
【题目】如图所示，水平面上有一质量
、长
的木板右端紧靠竖直墙壁，与墙壁不粘连，木板与水平面间的动摩擦因数
。质量
的小滑块（可视为质点）以水平速度
滑上木板左端，滑到木板右端时速度恰好为零，取重力加速度
。
(1)求小滑块与木板间的动摩擦因数μ2；
(2)现使小滑块以水平速度
滑上木板左端，滑到木板右端时与竖直墙壁发生碰撞（作用时间极短），碰后小滑块以原速率反弹。求：
①碰撞过程中，小滑块对墙壁的冲量I；
②最终小滑块停止运动时，木板右端离墙壁的距离s。
【答案】(1)0.8；(2)①80N·s，方向水平向右；②5m
【解析】
(1)小滑块以
滑上木板，滑到右端时速度恰好为零，根据动能定理有
代入数据解得
(2)①小滑块以
滑上木板，设滑到右端时速度大小为v，根据动能定理有
代入数据解得
小滑块与墙壁发生弹性碰撞，碰后速度大小仍为v，方向向左。以向左为正方向，对小滑块根据动量定理有
代入数据解得
由牛顿第三定律可知小滑块对墙壁的冲量
所以方向水平向右。
②碰后小滑块在木板上向左滑行，将木板带动，对小滑块根据牛顿第二定律有
代入数据解得
对木板有
代入数据解得
假设小滑块不会从木板上滑落，经过时间t，二者达到共同速度v共，则有
联立方程，代入数据解得
，
在时间t内，小滑块和木板向左运动的路程分别为sA和sB，小滑块在木板上滑行的距离为
，则有
联立方程，代入数据解得
因为
所以上述假设小滑块不会从板上滑落成立。经分析知共速后二者能一起向左做匀减速运动，根据牛顿第二定律有
代入数据解得
设木板向左匀减速滑行的路程为
，则
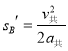
代入数据解得
最终小滑块停止运动时，木板右端离墙壁的距离为
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
