题目内容
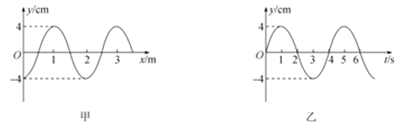
【题目】两根足够长的光滑平行金属轨道MN、PQ固定在倾角为θ的绝缘斜面上,相距为L,其电阻不计。长度为L、电阻为R的金属导体棒ab垂直于MN、PQ放在轨道上,与轨道接触良好。整个装置处于磁感应强度为B的匀强磁场中,磁场方向垂直于斜面向上。
如图1所示,若在轨道端点M、P之间接有阻值为R的电阻,则导体棒最终以速度v1沿轨道向下匀速运动;如图2所示,若在轨道端点M、P之间接有电动势为E,内阻为R的直流电源,则导体棒ab最终以某一速度沿轨道向上匀速运动。
(1)求图1导体棒ab最终匀速运动时电流的大小和方向以及导体棒ab两端的电势差;
(2)求图2导体棒ab最终沿轨道向上匀速运动的速度v2;
(3)从微观角度看,导体棒ab中的自由电荷所受洛伦兹力在能量转化中起着重要作用。我们知道,洛伦兹力对运动电荷不做功。那么,导体棒ab中的自由电荷所受洛伦兹力是如何在能量转化过程中起到作用的呢?请以图1导体棒ab最终匀速运动为例,通过计算分析说明。为了方便,可认为导体棒中的自由电荷为正电荷,如图3所示。
【答案】(1)![]() ,在导体棒ab内由b流向a,
,在导体棒ab内由b流向a,![]() (2)
(2)![]() (3)见解析
(3)见解析
【解析】(1)图1中,电路中的电流大小![]()
方向:在导体棒ab内由b流向a
导体棒ab两端的电势差 ![]()
(2)图1中,导体棒ab受力平衡 ![]()
图2中,导体棒ab受力平衡 ![]()
解得![]()
(3)如图所示,设自由电荷的电荷量为q,沿导体棒定向移动的速率为![]() 。
。
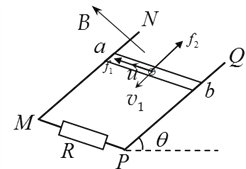
沿棒方向的洛伦兹力f1=qv1B,做正功
在Δt时间内,![]()
垂直棒方向的洛伦兹力f2=quB,做负功
在Δt时间内, ![]()
所以W1=-W2,
即导体棒中一个自由电荷所受的洛伦兹力做功为零。
f1做正功,驱动自由电荷定向移动,宏观上表现为“电动势”,使电能增加;f2做负功,宏观上表现为安培力做负功,消耗导体棒的机械能。大量自由电荷所受洛伦兹力做功的宏观表现是将机械能转化为等量的电能,在此过程中洛伦兹力通过两个分力做功起到“传递”能量的作用。