��Ŀ����
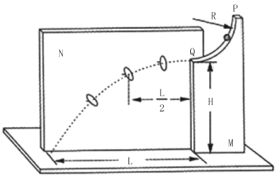
����Ŀ��ͬѧ�Dz���٤����ʱ����ʾƽ���˶��ķ�����������ͼ��ʾ��ʵ��װ�á�ͼ��ˮƽ���õĵװ�����ֱ�ع̶���M���N�塣M���ϲ���һ�뾶ΪR��![]() Բ���εĴֲڹ����PΪ��ߵ㣬QΪ��͵㣬Q�㴦������ˮƽ����װ��ΪH��N���Ϲ̶�������Բ���� ������Ϊm��С���P����ֹ�ͷţ�С���˶���Q�ɳ������谭��ͨ����Բ�����ģ��䵽�װ��Ͼ�Qˮƽ����ΪL���������ǿ����������������ٶ�Ϊg����
Բ���εĴֲڹ����PΪ��ߵ㣬QΪ��͵㣬Q�㴦������ˮƽ����װ��ΪH��N���Ϲ̶�������Բ���� ������Ϊm��С���P����ֹ�ͷţ�С���˶���Q�ɳ������谭��ͨ����Բ�����ģ��䵽�װ��Ͼ�Qˮƽ����ΪL���������ǿ����������������ٶ�Ϊg����
��1����Qˮƽ����Ϊ![]() ��Բ�����ĵ��װ�ĸ߶ȣ�
��Բ�����ĵ��װ�ĸ߶ȣ�
��2��С���˶���Q��ʱ�ٶȵĴ�С�Լ��Թ��ѹ���Ĵ�С��
��3��С���P��Q�Ĺ����п˷�Ħ���������Ĺ�![]() ��
��
���𰸡�(1)![]() ��(2)
��(2)![]() ��
��![]() ��(3)
��(3)![]()
��������
��1��С���Q�׳�����أ�����ƽ���˶����ɣ�����ֱ������
![]() ��
��
ˮƽ������
![]() ��
��
С���˶�����Qˮƽ����Ϊ![]() ��λ�ã�����ֱ������
��λ�ã�����ֱ������
![]() ��
��
ˮƽ������
![]() ��
��
�������Ϲ�ʽ�ɵ�![]()
Բ�����ĵ��װ�ĸ߶�Ϊ
![]()
��2���ɢ٢ڵ�С��Q����ٶ�
![]() ��
��
��Q����ţ�ٵڶ����ɵ�
![]() ��
��
�����ݢ�![]()
��ţ�ٵ������ɣ�С��Թ����ѹ���Ĵ�С![]()
��3��С���P��Q�Ĺ����У���������ϵ�ã�
![]() ��
��
�����ޢߵ�
![]()

��ϰ��ϵ�д�
�����Ŀ