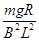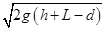题目内容
如上图所示,足够长且电阻不计的光滑平行金属导轨MN、PQ竖直放置,间距为L=0.5m,一匀强磁场B=0.2T垂直穿过导轨平面,导轨的上端M与P间连接阻值为R=0.40Ω的电阻,质量为m=0.01kg、 电阻不计的金属棒ab垂直紧贴在导轨上.现使金属棒ab由静止开始下滑,经过一段时间金属棒达到稳定状态,这段时间内通过R的电量0.3C,则在这一过程中( )(g=10m/s2 )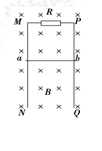
| A.安培力最大值为0.05N, |
| B.这段时间内下降的高度1.2m |
| C.重力最大功率为0.1w |
| D.电阻产生的焦耳热为0.04J |
BD
解析试题分析:安培力的最大值应该等于重力0.1N,故A错误;由法拉第电磁感应定律和闭合电路欧姆定律可知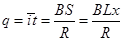 ,解得x=1.2m,故B正确;当安培力等于重力时,速度最大,
,解得x=1.2m,故B正确;当安培力等于重力时,速度最大,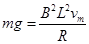 ,解得
,解得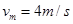 ,重力最大功率
,重力最大功率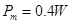 ,故C错误;由能量守恒定律,电阻产生的焦耳热
,故C错误;由能量守恒定律,电阻产生的焦耳热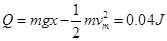 ,故D正确。
,故D正确。
考点:导体切割磁感线时的感应电动势;闭合电路的欧姆定律;电磁感应中的能量转化

如图所示,小明在玩蹦蹦杆。在小明将蹦蹦杆中的弹簧向下压缩的过程中,小明的重力势能、弹簧的弹性势能的变化是
| A.重力势能减小,弹性势能增大 |
| B.重力势能增大,弹性势能增大 |
| C.重力势能减小,弹性势能减小 |
| D.重力势能增大,弹性势能减小 |
质量为m的物块甲以3m/s的速度在光滑水平面上运动,有一轻弹簧固定其上,另一质量也为m的物体乙以4m/s的速度与甲相向运动,如图所示,则 ( )
| A.甲、乙两物块在弹簧压缩过程中,由于弹簧弹力的作用,甲乙两物体组成的系统动量不守恒 |
| B.当两物块相距最近时,甲物块的速度为零 |
| C.甲物块的速率可达到5m/s |
| D.当甲物块的速率为1m/s时,乙物块的速率可能为2m/s,也可能为0 |
如图所示,平行金属导轨宽度为L=0.6m,与水平面间的倾角为θ=37o,导轨电阻不计,底端接有阻值为R=3Ω的定值电阻,磁感应强度为B=1T的匀强磁场垂直向上穿过导轨平面。有一质量为m=0.2kg,长也为L的导体棒始终与导轨垂直且接触良好,导体棒的电阻为R0=1Ω,它与导轨之间的动摩擦因数为μ=0.3。现让导体棒从导轨底部以平行斜面的速度v0=10m/s向上滑行,上滑的最大距离为s=4m。 (sin37o=0.6,cos37o=0.8,g=10m/s2),以下说法正确的是( )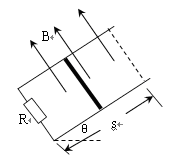
| A.把运动导体棒视为电源,最大输出功率6.75W |
| B.导体棒最后可以下滑到导轨底部,克服摩擦力做的总功为10.0J |
| C.当导体棒向上滑d=2m时,速度为7.07m/s |
| D.导体棒上滑的整个过程中,在定值电阻R上产生的焦耳热为2.46J |
如图甲所示,静止在地面上的一个物体在竖直向止的拉力作用下开始运动在,向上运动的过程中,物体的动能Ek与位移x关系图象如图乙所示。其中在0~h过程中的图线为平滑曲线,h~2h过程中的图线为平行于横轴的直线,2h~3h过程中的图线为一倾斜的直线,不计空气阻力,下列说法正确的是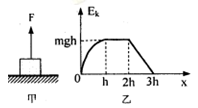
| A.物体上升到h高处时,拉力的功率为零 |
| B.在0~h过程中拉力大小恒为2mg |
| C.在h~23h过程中物体机械能不变 |
| D.在2h~3h过程中物体的机械能不变 |
如图,足够长的光滑导轨倾斜放置,导轨宽度为L,,其下端与电阻R连接;导体棒ab电阻为r,导轨和导线电阻不计,匀强磁场竖直向上。若导体棒ab以一定初速度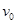 下滑,则ab棒
下滑,则ab棒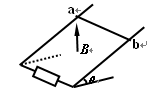
| A.所受安培力方向水平向右 |
B.可能以速度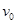 匀速下滑 匀速下滑 |
C.刚下滑瞬间产生的电动势为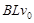 |
| D.减少的重力势能等于电阻R产生的内能 |
如图所示,电阻不计的竖直光滑金属轨道PMNQ,其PMN部分是半径为r的1/4圆弧,NQ部分水平且足够长,匀强磁场的磁感应强度为B,方向垂直于PMNQ平面指向纸里.一粗细均匀的金属杆质量为m,电阻为R,长为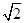 r,从图示位置由静止释放,若当地的重力加速度为g,金属杆与轨道始终保持良好接触,则( )
r,从图示位置由静止释放,若当地的重力加速度为g,金属杆与轨道始终保持良好接触,则( )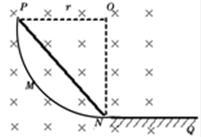
| A.杆下滑过程机械能守恒 |
| B.杆最终可能沿NQ匀速运动 |
| C.杆从释放到滑至水平轨道过程产生的电能大于mgR/2 |
D.杆从释放到滑至水平轨道过程中,通过杆的电荷量等于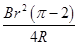 |
 d
d