题目内容
 (2013?南昌二模)如图所示,AOB是由某种透明物质制成的
(2013?南昌二模)如图所示,AOB是由某种透明物质制成的| 1 |
| 4 |
| 2 |
60°
60°
,圆柱AB面上能射出光线的部分占AB表面的| 1 |
| 2 |
| 1 |
| 2 |
分析:画出光路图,根据折射定律和几何关系求解进入圆柱的折射光线与OA间的夹角;
当光线在AB弧面上发生全反射时,就没有光线从AB弧面射出,根据临界角确定出光线在AB弧面上恰好发生全反射时的入射点,由几何知识求解圆柱AB面上能射出光线的面积占AB表面积的几分之几.
当光线在AB弧面上发生全反射时,就没有光线从AB弧面射出,根据临界角确定出光线在AB弧面上恰好发生全反射时的入射点,由几何知识求解圆柱AB面上能射出光线的面积占AB表面积的几分之几.
解答: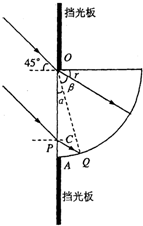 解:从O点射入的光线,折射角为r,根据折射定律有:n=
解:从O点射入的光线,折射角为r,根据折射定律有:n=
=
解得:r=30°
由几何关系得知进入圆柱的折射光线与OA间的夹角为 60°.
从某位置P点入射的光线,折射到AB弧面上Q点时,入射角恰等于临界角C,有:sinC=
=
得:C=45° ④
在△PQO中,∠α=180°-90°-r-C=15°
所以能射出的光线区域对应的圆心角 β=90°-α-r=45°
所以能射出光线的部分占AB面的比例为
=
.
故答案为:60°,
 解:从O点射入的光线,折射角为r,根据折射定律有:n=
解:从O点射入的光线,折射角为r,根据折射定律有:n=| sin45° |
| sinr |
| 2 |
解得:r=30°
由几何关系得知进入圆柱的折射光线与OA间的夹角为 60°.
从某位置P点入射的光线,折射到AB弧面上Q点时,入射角恰等于临界角C,有:sinC=
| 1 |
| n |
| 1 | ||
|
得:C=45° ④
在△PQO中,∠α=180°-90°-r-C=15°
所以能射出的光线区域对应的圆心角 β=90°-α-r=45°
所以能射出光线的部分占AB面的比例为
| 45° |
| 90° |
| 1 |
| 2 |
故答案为:60°,
| 1 |
| 2 |
点评:正确地画出光路图是解决本题问题的关键,是折射定律和几何知识的综合应用.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
 (2013?南昌二模)一列简谐横波沿直线传播,在波的传播方向上有P、Q两个质点,它们相距 0.8m,当t=0时,P、Q两点位移恰好都是正的最大值,且P、Q间只有一个波谷.当t=0.6s时,P、Q两点正好都处于平衡位置,且P、Q两点间有一个波峰和一个波谷,且波峰距Q点为0.2m,试求:
(2013?南昌二模)一列简谐横波沿直线传播,在波的传播方向上有P、Q两个质点,它们相距 0.8m,当t=0时,P、Q两点位移恰好都是正的最大值,且P、Q间只有一个波谷.当t=0.6s时,P、Q两点正好都处于平衡位置,且P、Q两点间有一个波峰和一个波谷,且波峰距Q点为0.2m,试求:

 (2013?南昌二模)如图所示,相隔-定距离的两个相同圆柱体固定在同-水平高度处,一轻绳套在两圆柱体上,轻绳下端悬挂一重物,绳和圆柱体之间的摩擦忽略不计.现增加轻绳长度,而其他条件保持不变,则( )
(2013?南昌二模)如图所示,相隔-定距离的两个相同圆柱体固定在同-水平高度处,一轻绳套在两圆柱体上,轻绳下端悬挂一重物,绳和圆柱体之间的摩擦忽略不计.现增加轻绳长度,而其他条件保持不变,则( )