��Ŀ����
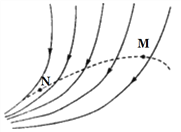
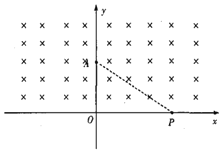
����Ŀ����ͼ��ʾ����ƽ��ֱ������ϵ�У�x���Ϸ����������ǿ�ų����ų�����ֱ������ϵƽ�����y�������������r��A����һ���ӷ���Դ������ų����������ز�ͬ�����������Ϊm�������Ϊ-q�����ӣ������ٶȴ�С��ͬ������Щ���Ӿ���x���ϵ����е�����P��������ԭ�������Զ���������Ϊ![]() r��������˵������ȷ���ǣ�������
r��������˵������ȷ���ǣ�������
A. �����ڴų����˶�����P��ʱ���˶��켣��x������
B. �����ڴų����˶���ʱ�����ʱ���˶��켣��x������
C. �����ڴų����˶��Ĺ���뾶����![]() r
r
D. ������x�Ḻ�������ܾ�������Զ����������-r
���𰸡�D
���������������⣬�����ڴų����˶����Բ�ܺ���x��Ľ�����ԭ�������Զ���켣��ͼ��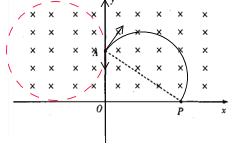
��Ȼ���˶��켣�Ͳ���x�����У���A�����ݼ��ι�ϵ֪�� ![]() ����ã�R=r�������ڴų����˶��Ĺ���뾶����r����C���������ٶȷ�����y�Ḻ����ʱ��������x�Ḻ�������У��ܾ�������Զ��ĺ�����Ϊ-r����D��ȷ�����ӵ��˶��켣�ǹ���0��r�����ҹ켣�뾶Ϊr��˳ʱ��Ķ�̬Բ����ͼ֪��ʱ�����ʱ��Բ���ij�����̣��˶��켣��x������У���B����ѡD��
����ã�R=r�������ڴų����˶��Ĺ���뾶����r����C���������ٶȷ�����y�Ḻ����ʱ��������x�Ḻ�������У��ܾ�������Զ��ĺ�����Ϊ-r����D��ȷ�����ӵ��˶��켣�ǹ���0��r�����ҹ켣�뾶Ϊr��˳ʱ��Ķ�̬Բ����ͼ֪��ʱ�����ʱ��Բ���ij�����̣��˶��켣��x������У���B����ѡD��

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ