题目内容
15.在连云港市青年公园的游乐场中,有一台大型游乐机叫“垂直极限”.一质量为60kg的游客被安全带固定在座椅上,由电动机将座椅提升到一定高度处,座椅沿光滑杆自由下落1.2s 后开始受到压缩空气提供的恒定阻力作用做匀减速直线运动,又经4.8s速度刚好减为零.这一过程座椅共下落了36m.已知重力加速度g=10m/s2.求:(1)座椅下落过程的平均速度;
(2)座椅被释放后,自由下落的高度;
(3)在减速阶段,座椅对游客的支持力.
分析 (1)由平均速度的定义式即可求出平均速度;
(2)根据位移时间关系公式列式求解即可;
(3)先根据速度关系公式求解加速度,然后受力分析并根据牛顿第二定律列式求解.
解答 解:(1)已知下降的高度与时间,则平均速度:$\overline{v}=\frac{h}{{t}_{1}+{t}_{2}}=\frac{36}{1.2+4.8}=6$m/s
(2)座椅释放后自由下落的高度为h1,速度为v,减速下落的高度为h2:
自由下落的位移:${h}_{1}=\frac{1}{2}g{t}_{1}^{2}=\frac{1}{2}×10×1.{2}^{2}=7.2$m,
(3)减速阶段的初速度为加速阶段的末速度,所以两段时间内的速度变化大小相等;
由速度公式得:v=gt1,0=v+at2,
代入数据得减速阶段,座椅的加速度是:a=2.5m/s2
设游客的质量为m,座椅对游客的支持力为F,
由牛顿第二定律得:
F-mg=ma,
得:F=m(g+a)=60×(10+2.5)750N
答:(1)座椅下落过程的平均速度是6m/s;
(2)座椅被释放后,自由下落的高度是7.2m;
(3)在减速阶段,座椅对游客的支持力是750N.
点评 本题涉及两个过程,关键根据运动学公式确定加速度,然后根据牛顿第二定律确定受力情况,中档题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5. 如图所示,一电容为C的平行板电容器,两极板A、B间距离为d,板间电压为U,B板电势高于A板.两板间有M、N、P三点,MN连线平行于极板,N、P连线垂直于极板,M、P两点间距离为L,∠PMN=θ.以下说法正确的是( )
如图所示,一电容为C的平行板电容器,两极板A、B间距离为d,板间电压为U,B板电势高于A板.两板间有M、N、P三点,MN连线平行于极板,N、P连线垂直于极板,M、P两点间距离为L,∠PMN=θ.以下说法正确的是( )
 如图所示,一电容为C的平行板电容器,两极板A、B间距离为d,板间电压为U,B板电势高于A板.两板间有M、N、P三点,MN连线平行于极板,N、P连线垂直于极板,M、P两点间距离为L,∠PMN=θ.以下说法正确的是( )
如图所示,一电容为C的平行板电容器,两极板A、B间距离为d,板间电压为U,B板电势高于A板.两板间有M、N、P三点,MN连线平行于极板,N、P连线垂直于极板,M、P两点间距离为L,∠PMN=θ.以下说法正确的是( )| A. | 电容器带电量为$\frac{U}{C}$ | |
| B. | 两极板间匀强电场的电场强度大小为$\frac{U}{d}$ | |
| C. | M、P两点间的电势差为$\frac{UL}{d}$ | |
| D. | 若将带电量为+q的电荷从M移到P,该电荷的电势能减少了$\frac{qULsinθ}{d}$ |
6. 摆式列车是集电脑、自动控制等高新技术于一体的新型高速列车,如图所示.当列车转弯时在电脑控制下车厢会自动倾斜,沿直线行驶时车厢又恢复成竖直状态,就像玩具“不倒翁”一样假设有一超高速列车在水平面内行驶,以360km/h的速度拐弯,拐弯半径为1km,则车厢内质量为50kg的乘客,在拐弯过程中受到火车给他的作用力为(g取l0m/s2)( )
摆式列车是集电脑、自动控制等高新技术于一体的新型高速列车,如图所示.当列车转弯时在电脑控制下车厢会自动倾斜,沿直线行驶时车厢又恢复成竖直状态,就像玩具“不倒翁”一样假设有一超高速列车在水平面内行驶,以360km/h的速度拐弯,拐弯半径为1km,则车厢内质量为50kg的乘客,在拐弯过程中受到火车给他的作用力为(g取l0m/s2)( )
 摆式列车是集电脑、自动控制等高新技术于一体的新型高速列车,如图所示.当列车转弯时在电脑控制下车厢会自动倾斜,沿直线行驶时车厢又恢复成竖直状态,就像玩具“不倒翁”一样假设有一超高速列车在水平面内行驶,以360km/h的速度拐弯,拐弯半径为1km,则车厢内质量为50kg的乘客,在拐弯过程中受到火车给他的作用力为(g取l0m/s2)( )
摆式列车是集电脑、自动控制等高新技术于一体的新型高速列车,如图所示.当列车转弯时在电脑控制下车厢会自动倾斜,沿直线行驶时车厢又恢复成竖直状态,就像玩具“不倒翁”一样假设有一超高速列车在水平面内行驶,以360km/h的速度拐弯,拐弯半径为1km,则车厢内质量为50kg的乘客,在拐弯过程中受到火车给他的作用力为(g取l0m/s2)( )| A. | 0 | B. | 500N | C. | 500$\sqrt{2}$N | D. | l000N |
3.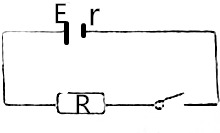 电阻R值为2Ω,将其与电动势为E=3V,内阻为r的电源串联如图,当R连按到内阻为多少的电源两端时R消耗的功率最大?
电阻R值为2Ω,将其与电动势为E=3V,内阻为r的电源串联如图,当R连按到内阻为多少的电源两端时R消耗的功率最大?
 电阻R值为2Ω,将其与电动势为E=3V,内阻为r的电源串联如图,当R连按到内阻为多少的电源两端时R消耗的功率最大?
电阻R值为2Ω,将其与电动势为E=3V,内阻为r的电源串联如图,当R连按到内阻为多少的电源两端时R消耗的功率最大?| A. | r=0.5Ω | B. | r=1Ω | C. | r=2Ω | D. | r=3Ω |
20.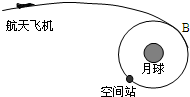 我国未来将建立月球基地,并在绕月轨道上建造空间站.如图所示,关闭动力的航天飞船在月球引力作用下向月球靠近,并将沿椭圆轨道与空间站在B处对接,已知空间站绕月轨道半径为r,周期为T,引力常量为G,月球的半径为R,下列说法中正确的是( )
我国未来将建立月球基地,并在绕月轨道上建造空间站.如图所示,关闭动力的航天飞船在月球引力作用下向月球靠近,并将沿椭圆轨道与空间站在B处对接,已知空间站绕月轨道半径为r,周期为T,引力常量为G,月球的半径为R,下列说法中正确的是( )
 我国未来将建立月球基地,并在绕月轨道上建造空间站.如图所示,关闭动力的航天飞船在月球引力作用下向月球靠近,并将沿椭圆轨道与空间站在B处对接,已知空间站绕月轨道半径为r,周期为T,引力常量为G,月球的半径为R,下列说法中正确的是( )
我国未来将建立月球基地,并在绕月轨道上建造空间站.如图所示,关闭动力的航天飞船在月球引力作用下向月球靠近,并将沿椭圆轨道与空间站在B处对接,已知空间站绕月轨道半径为r,周期为T,引力常量为G,月球的半径为R,下列说法中正确的是( )| A. | 航天飞机到达B处由椭圆轨道进入空间站轨道时必须加速 | |
| B. | 航天飞船在B处由椭圆轨道进入空间站轨道必须点火减速 | |
| C. | 月球的质量为M=$\frac{4{π}^{2}{r}^{3}}{G{T}^{2}}$ | |
| D. | 月球的第一宇宙速度为V=$\frac{2πr}{T}$ |
1.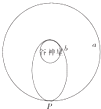 历时8年,跋涉48亿公里的“黎明”号飞行器于2015年3月7日首次抵达太阳系的小行星带内质量最大的天体--谷神星,“黎明”号飞行器绕谷神星做匀速圆周运动,已知引力常量为G,下列说法正确的是( )
历时8年,跋涉48亿公里的“黎明”号飞行器于2015年3月7日首次抵达太阳系的小行星带内质量最大的天体--谷神星,“黎明”号飞行器绕谷神星做匀速圆周运动,已知引力常量为G,下列说法正确的是( )
 历时8年,跋涉48亿公里的“黎明”号飞行器于2015年3月7日首次抵达太阳系的小行星带内质量最大的天体--谷神星,“黎明”号飞行器绕谷神星做匀速圆周运动,已知引力常量为G,下列说法正确的是( )
历时8年,跋涉48亿公里的“黎明”号飞行器于2015年3月7日首次抵达太阳系的小行星带内质量最大的天体--谷神星,“黎明”号飞行器绕谷神星做匀速圆周运动,已知引力常量为G,下列说法正确的是( )| A. | 若测得飞行器围绕谷神星旋转的圆轨道的周期和轨道半径,可得到谷神星的平均密度 | |
| B. | 飞行器轨道半径越大,运行周期越大 | |
| C. | 飞行器轨道半径越大,线速度越大 | |
| D. | 图示中飞行器由环谷神星圆轨道a“变轨进入环谷神星椭圆轨道b时,应让发动机在P点点火使其加速 |
18.如图,近地人造卫星和月球绕地球的运行轨道可视为圆.下列说法正确的是( )
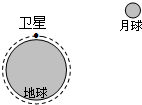

| A. | 卫星、月球绕地运行周期T卫>T月 | B. | 卫星、月球绕地运行周期T卫=T月 | ||
| C. | 卫星、月球绕地运行线速度v卫<v月 | D. | 卫星、月球绕地运行线速度v卫>v月 |
 在地面附近的真空环境中,建立一直角坐标系,y轴正方向竖直向上,x轴正方向水平向右,空间有沿水平方向且垂直于xOy平面指向读者的匀强磁场(磁感强度B=0.25T)和沿x轴正方向的匀强电场(场强E=2N/C),如图所示,一个质量m=$\sqrt{3}$×10-7kg,电量q=5×10-7C的带负电微粒,在此区域中刚好沿直线运动(g取10m/s2).
在地面附近的真空环境中,建立一直角坐标系,y轴正方向竖直向上,x轴正方向水平向右,空间有沿水平方向且垂直于xOy平面指向读者的匀强磁场(磁感强度B=0.25T)和沿x轴正方向的匀强电场(场强E=2N/C),如图所示,一个质量m=$\sqrt{3}$×10-7kg,电量q=5×10-7C的带负电微粒,在此区域中刚好沿直线运动(g取10m/s2).