题目内容
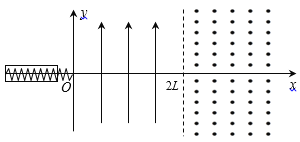
【题目】如图所示,在光滑的水平地面上建立直角坐标系xOy,0<x<2L的区域内有一沿y轴正方向的匀强电场,x>2L的区域内有一竖直向上的匀强磁场。x轴的负半轴上固定一 弹射装置,弹簧的自由端刚好位于坐标原点。某时刻,将一带正电的小球压缩弹簧装入弹射装置,小球被弹射后以速度v0进入电场;之后的另一时刻,另一质量相同的带负电小球也被弹射后以同样的速度进入电场,其进入磁场边界时的坐标为(2L,-![]() L)。负电小球所带电荷量大小是正电小球的3倍,它们在磁场中分别运动半周后在某点相遇,不计两小球之间的相互作用,求:
L)。负电小球所带电荷量大小是正电小球的3倍,它们在磁场中分别运动半周后在某点相遇,不计两小球之间的相互作用,求:
(1)负电小球进入磁场边界时速度方向与y轴负方向的夹角;
(2)两小球在磁场中相遇时的位置坐标;
(3)两小球先后进入电场的时间差。
【答案】(1)![]() ,
,![]() (2)(3L,-
(2)(3L,-![]() )(3)
)(3)![]()
【解析】
(1)负电小球在电场中做类平抛运动,根据两个方向的运动特征求解小球进入磁场边界时速度方向与y轴负方向的夹角;(2)由于负电小球所带电荷量大小是正电小球的3倍,正电小球在电场中做类平抛运动的加速度为负电小球的1/3倍;进入磁场时的纵坐标为负电小球的1/3倍,根据几何关系求解两小球在磁场中相遇时的位置坐标;(3)根据粒子在磁场中做圆周运动的周期求解两小球先后进入电场的时间差。
(1)负电小球在电场中做类平抛运动,有
![]()
![]()
由以上两式可得![]()
设小球进入磁场边界时速度方向与y轴负方向的夹角为θ2,有
![]()
![]()
(2)由于负电小球所带电荷量大小是正电小球的3倍,正电小球在电场中做类平抛运动的加速度为负电小球的1/3倍;进入磁场边界时的坐标为(2L,![]() )
)
设正电小球进入磁场边界时速度方向与y轴正方向的夹角为θ1,可解得
![]()
由几何关系可知,两小球相遇点和正负小球进入磁场边界时的位置构成直角三角形,设相遇点的位置坐标为(x,y),有
![]()
![]()
(3)两小球在电场中运动的时间相等,设正电小球在磁场中运动半周的时间为t1,速度为v1,负电小球在磁场中运动半周的时间为t2,速度为v2,则
![]()
![]()
![]()
![]()
因此,要使两小球相遇,两小球先后进入电场的时间差为
![]()

 阅读快车系列答案
阅读快车系列答案