题目内容
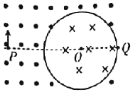
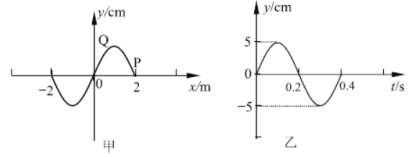
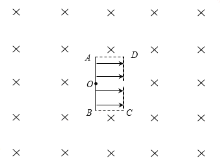
【题目】如图所示,两块平行极板AB、CD正对放置,极板CD的正中央有一小孔,两极板间距离AD为d,板长AB为2d,两极板间电势差为U,在ABCD构成的矩形区域内存在匀强电场,电场方向水平向右。在ABCD矩形区域外有垂直于纸面向里的范围足够大的匀强磁场。极板厚度不计,电场、磁场的交界处为理想边界。将一个质量为m、电荷量为+q的带电粒子在极板AB的正中央O点由静止释放。不计带电粒子的重力。
(1)为了使带电粒子能够再次进入匀强电场,且进入电场时的速度方向与电场方向垂直,求磁场的磁感应强度的大小;
(2)通过分析说明带电粒子第二次离开电场时的位置,并求出带电粒子从O点开始运动到第二次离开电场区域所经历的总时间;
(3)通过分析说明带电粒子最后能否返回最初的出发点O,并画出粒子运动轨迹的示意图。若能返回O点,试求出带电粒子从O点开始运动到最终返回O点所经历的总时间。
【答案】(1)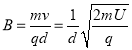 ;(2)从C点射出,
;(2)从C点射出,![]() ; (3)
; (3) 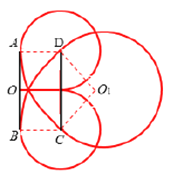 ,
,![]()
【解析】
(1)设带电粒子经过电场加速后,从极板CD正中央的小孔射出时的速度大小为v
![]()
带电粒子第一次从电场中射出后,在磁场中做匀速圆周运动,若能够再进入匀强电场,且进入电场时的速度方向与电场方向垂直,运动向改变![]() ,由此可知在场中的运动轨迹为四分之三圆,圆心位于D点,半径为d,由A点垂直射入电场,如图:
,由此可知在场中的运动轨迹为四分之三圆,圆心位于D点,半径为d,由A点垂直射入电场,如图:

带电粒子在磁场中运动时,洛伦兹力充当向心力,由牛顿运动定律得
![]()
解得
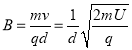
(2)带电粒子由A点垂直于电场方向射入电场之后做类平抛运动
若能够射出电场,运动时间

沿电场方向的位移
![]()
有
![]()
解得
![]()
因此带电粒子恰能从C点射出。
带电粒子在磁场中偏转,运动时间为![]() ,洛伦兹力充当向心力
,洛伦兹力充当向心力
由牛顿第二定律得
![]()
解得
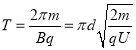
设带电粒子在磁场中偏转运动时间为![]() ,有
,有
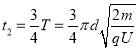
带电粒子第一次在电场中加速运动时间也为![]() ,因此带电粒子从O点运动到C点的总时间
,因此带电粒子从O点运动到C点的总时间
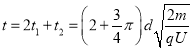
(3)带电粒子第二次离开电场时的速度为
![]()
设粒子离开电场时的偏转角度![]() ,则
,则
![]()
解得
![]()
由此可知在磁场中的运动轨迹为四分之三圆。
第二次在磁场中做圆周运动的向心力由洛伦兹力提供,得
![]()
解得
![]()
粒子到达CD连时与C点的距离
![]()
因此带电粒子恰能从D点射入电场。
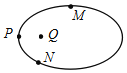
根据对称性可知,带电粒子第三次离开电场的位置恰好是在B点,速度是v,方向与BC连垂直,然后以C点为圆心,半径d做圆周运动,从CD的中点第三次进入电场,最终刚好返回O点。粒子运动轨迹的示意图如图所示:

粒子从O点出发返回到O的过程中,四次进出电场,三次在磁场中做四分之三的圆周运动。带电粒子运动的总时间
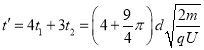

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案