题目内容
14.若有一颗行星,其质量为地球质量的p倍,半径为地球半径的q倍,则该行星第一宇宙速度是地球第一宇宙速度的( )| A. | $\sqrt{pq}$倍 | B. | $\sqrt{\frac{q}{p}}$倍 | C. | $\sqrt{\frac{p}{q}}$倍 | D. | $\sqrt{p{q}^{3}}$倍 |
分析 根据万有引力提供圆周运动向心力求得第一宇宙速度的表达式,再根据质量和半径关系求行星的第一宇宙速度.
解答 解:令地球质量为M,半径为R,则行星的质量为PM,半径为qR,
第一宇宙速度是近地卫星的绕行速度,根据万有引力提供圆周运动向心力有:
$G\frac{mM}{{R}^{2}}=m\frac{{v}^{2}}{R}$
可得地球第一宇宙速度表达式为v=$\sqrt{\frac{GM}{R}}$
同理行星的第一宇宙速度表达式为:v$′=\sqrt{\frac{GPM}{qR}}=\sqrt{\frac{P}{q}}•\sqrt{\frac{GM}{R}}$
故选:C.
点评 本题要掌握第一宇宙速度的定义,正确利用万有引力公式列出第一宇宙速度的表达式是正确解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.在做“研究平抛物体的运动”实验时,除了木板、小球、斜槽、铅笔、图钉之外,下列器材中还需要的是( )
| A. | 重垂线 | B. | 秒表 | C. | 坐标纸或白纸 | D. | 天平 |
2.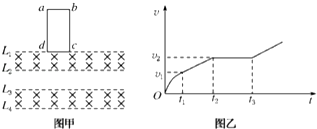 如图甲所示,在竖直方向上有四条间距相等的水平虚线L1、L2、L3、L4,在L1L2之间、L3L4之间存在匀强磁场,大小均为1T,方向垂直于虚线所在平面.现有一矩形线圈abcd,宽度cd=L=0.5m,质量为0.1kg,电阻为2Ω,将其从图示位置静止释放(cd边与L1重合),速度随时间的变化关系如图乙所示,t1时刻cd边与L2重合,t2时刻ab边与L3重合,t3时刻ab边与L4重合,已知t1~t2的时间间隔为0.6s,整个运动过程中线圈平面始终处于竖直方向.(重力加速度g取10m/s2)则( )
如图甲所示,在竖直方向上有四条间距相等的水平虚线L1、L2、L3、L4,在L1L2之间、L3L4之间存在匀强磁场,大小均为1T,方向垂直于虚线所在平面.现有一矩形线圈abcd,宽度cd=L=0.5m,质量为0.1kg,电阻为2Ω,将其从图示位置静止释放(cd边与L1重合),速度随时间的变化关系如图乙所示,t1时刻cd边与L2重合,t2时刻ab边与L3重合,t3时刻ab边与L4重合,已知t1~t2的时间间隔为0.6s,整个运动过程中线圈平面始终处于竖直方向.(重力加速度g取10m/s2)则( )
 如图甲所示,在竖直方向上有四条间距相等的水平虚线L1、L2、L3、L4,在L1L2之间、L3L4之间存在匀强磁场,大小均为1T,方向垂直于虚线所在平面.现有一矩形线圈abcd,宽度cd=L=0.5m,质量为0.1kg,电阻为2Ω,将其从图示位置静止释放(cd边与L1重合),速度随时间的变化关系如图乙所示,t1时刻cd边与L2重合,t2时刻ab边与L3重合,t3时刻ab边与L4重合,已知t1~t2的时间间隔为0.6s,整个运动过程中线圈平面始终处于竖直方向.(重力加速度g取10m/s2)则( )
如图甲所示,在竖直方向上有四条间距相等的水平虚线L1、L2、L3、L4,在L1L2之间、L3L4之间存在匀强磁场,大小均为1T,方向垂直于虚线所在平面.现有一矩形线圈abcd,宽度cd=L=0.5m,质量为0.1kg,电阻为2Ω,将其从图示位置静止释放(cd边与L1重合),速度随时间的变化关系如图乙所示,t1时刻cd边与L2重合,t2时刻ab边与L3重合,t3时刻ab边与L4重合,已知t1~t2的时间间隔为0.6s,整个运动过程中线圈平面始终处于竖直方向.(重力加速度g取10m/s2)则( )| A. | 在0~t1时间内,通过线圈的电荷量为0.25C | |
| B. | 线圈匀速运动的速度大小为8m/s | |
| C. | 线圈的长度为1m | |
| D. | 0~t3时间内,线圈产生的热量为4.2J |
6.如图所示,一木块在竖直向下的推力F作用下静止于斜面上,则下列判断正确的是( )


| A. | 木块可能受三个力作用 | |
| B. | 若推力F逐渐增大,木块将可能滑动 | |
| C. | 斜面所受摩擦力方向沿斜面向上 | |
| D. | 木块受斜面的摩擦力会随推力F的增大而增大 |
 如图所示:图线a是某电源的外特性曲线,图线b是电阻R的伏安特性曲线,这个电源的内阻等于2Ω.用这个电源和两个电阻R串联形成闭合电路,电源的输出功率为4W.
如图所示:图线a是某电源的外特性曲线,图线b是电阻R的伏安特性曲线,这个电源的内阻等于2Ω.用这个电源和两个电阻R串联形成闭合电路,电源的输出功率为4W. 如图所示为研究电子枪中电子在电场中运动的简化模型示意图.在Oxy平面的ABCD区域内,存在两个场强大小均为E的匀强电场Ⅰ和Ⅱ,两电场的边界均是边长为三的正方形(不计电子所受重力)已知电子的质量为肌,电荷量的大小为e,求:
如图所示为研究电子枪中电子在电场中运动的简化模型示意图.在Oxy平面的ABCD区域内,存在两个场强大小均为E的匀强电场Ⅰ和Ⅱ,两电场的边界均是边长为三的正方形(不计电子所受重力)已知电子的质量为肌,电荷量的大小为e,求: 神秘的黑洞是近代引力理论所预言的一种特殊天体,探寻黑洞的方案之一是观测双星系统的运动规律.天文学家观测河外星系大麦哲伦云时,发现了LMCX-3双星系统,它由可见星A和不可见的暗星B构成,两星可视为质点,不考虑其他天体的影响,A、B围绕两者连线上的O点做匀速圆周运动,它们之间的距离保持不变,如图所示.
神秘的黑洞是近代引力理论所预言的一种特殊天体,探寻黑洞的方案之一是观测双星系统的运动规律.天文学家观测河外星系大麦哲伦云时,发现了LMCX-3双星系统,它由可见星A和不可见的暗星B构成,两星可视为质点,不考虑其他天体的影响,A、B围绕两者连线上的O点做匀速圆周运动,它们之间的距离保持不变,如图所示.