题目内容
(20分)如图所示,在高为h的平台上,距边缘为L处有一质量为M的静止木块(木块的尺度比L小得多),一颗质量为m的子弹以初速度v0射入木块中未穿出,木块恰好运动到平台边缘未落下,若将子弹的速度增大为原来的两倍而子弹仍未穿出,求木块的落地点距平台边缘的水平距离,设子弹打入木块的时间极短。

解析:
设子弹以v0射入时,木块的初速度为v1,根据动量守恒定律有
mv0=(m+M) v1 ①
根据动能定理有 μ(m+M)gL=![]() (m+M)v12 ②
(m+M)v12 ②
设子弹以2v0射入时,木块的初速度为v2,末速度为v3,根据动量守恒定律有
m2v0=(m+M) v2 ③
根据动能定理有 μ(m+M)gL=![]() (m+M)v22-
(m+M)v22-![]() (m+M)v32 ④
(m+M)v32 ④
设木块落地点距平台边缘的距离为x,由平抛运动规律有
X= v3![]() ⑤
⑤
由①②③④⑤联立解得 x=![]()

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
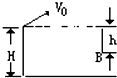 如图所示,在高为H的平台上以初速V0抛出一质量为m的小球,不计空气阻力,当它到达离抛出点的竖直距离为h的B点时,小球的动能增量为( )
如图所示,在高为H的平台上以初速V0抛出一质量为m的小球,不计空气阻力,当它到达离抛出点的竖直距离为h的B点时,小球的动能增量为( )A、
| ||
B、
| ||
C、
| ||
| D、mgh |
 如图所示,在高为h的光滑固定不动的平台上放一个质量为m2的小球,另一个质量为 m1的球沿光滑固定不动的弧形轨道从距平台高为h处由静止开始下滑,滑至平台上与球m2发生正碰,若m1=m2=m,求小球m2最终落点距平台右边缘水平距离的取值范围.
如图所示,在高为h的光滑固定不动的平台上放一个质量为m2的小球,另一个质量为 m1的球沿光滑固定不动的弧形轨道从距平台高为h处由静止开始下滑,滑至平台上与球m2发生正碰,若m1=m2=m,求小球m2最终落点距平台右边缘水平距离的取值范围. 如图所示,在高为h的木箱abcd的水平底板上静置着一个质量为m的小物块A,现用一电动机向上拉木箱,使木箱由静止开始向上运动,且保持电动机的输出功率不变,经时间t木箱达到最大速度,若此时让木箱突然停止运动,小物块由于惯性会继续向上运动,且恰好到达木箱的顶端,空气阻力不计,木箱和小物块的总质量为M,重力加速度为g,求:
如图所示,在高为h的木箱abcd的水平底板上静置着一个质量为m的小物块A,现用一电动机向上拉木箱,使木箱由静止开始向上运动,且保持电动机的输出功率不变,经时间t木箱达到最大速度,若此时让木箱突然停止运动,小物块由于惯性会继续向上运动,且恰好到达木箱的顶端,空气阻力不计,木箱和小物块的总质量为M,重力加速度为g,求: 如图所示,在高为H的平台上以初速v0抛出一质量为m的小球,不计空气阻力,当它到达离抛出点的竖直距离为h的B点时,小球的动能增量为( )
如图所示,在高为H的平台上以初速v0抛出一质量为m的小球,不计空气阻力,当它到达离抛出点的竖直距离为h的B点时,小球的动能增量为( ) 如图所示,在高为h的平台边缘水平抛出小球A,同时在水平地面上距台面边缘水平距离为s处竖直上抛小球B,两球运动轨迹在同一竖直平面内,不计空气阻力,重力加速度为g.若两球能在空中相遇,则小球A的初速度VA应大于
如图所示,在高为h的平台边缘水平抛出小球A,同时在水平地面上距台面边缘水平距离为s处竖直上抛小球B,两球运动轨迹在同一竖直平面内,不计空气阻力,重力加速度为g.若两球能在空中相遇,则小球A的初速度VA应大于