题目内容
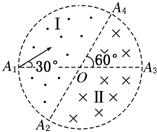 如图所示,在一个圆形区域内,两个方向相反且都垂直于纸面的匀强磁场分布在以直径A2A4为边界的两个半圆形区域Ⅰ、Ⅱ中,直径A2A4与A1A3的夹角为60°.一质量为m、带电荷量为+q的粒子以某一速度从Ⅰ区的边缘点A1处沿与A1A3成30°角的方向射入磁场,随后该粒子以垂直于A2A4的方向经过圆心O进入Ⅱ区,最后从A4处射出磁场.已知该粒子从射入到射出磁场所用的时间为t.(忽略粒子重力).
如图所示,在一个圆形区域内,两个方向相反且都垂直于纸面的匀强磁场分布在以直径A2A4为边界的两个半圆形区域Ⅰ、Ⅱ中,直径A2A4与A1A3的夹角为60°.一质量为m、带电荷量为+q的粒子以某一速度从Ⅰ区的边缘点A1处沿与A1A3成30°角的方向射入磁场,随后该粒子以垂直于A2A4的方向经过圆心O进入Ⅱ区,最后从A4处射出磁场.已知该粒子从射入到射出磁场所用的时间为t.(忽略粒子重力).(1)求粒子在Ⅰ区和Ⅱ区中的速度偏角φ1和φ2
(2)求Ⅰ区和Ⅱ区中磁感应强度的大小B1和B2.
分析:由题意可知粒子在两磁场中的转动轨迹,由几何关系可知两圆的半径,则由洛仑兹力充当向心力可列出方程;再根据在两磁场中转过的圆心角可求得在两磁场中的时间,则由两粒子在两磁场中运动的总时间可列出关于时间的表达式,联立可解得磁感应强度.
解答:解: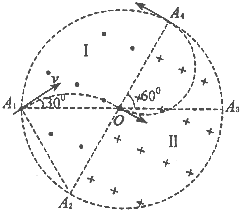 设粒子的入射速度为v,已知粒子带正电,故它在磁场中先顺时针做圆周运动,再逆时针做圆周运动,最后从A4点射出,
设粒子的入射速度为v,已知粒子带正电,故它在磁场中先顺时针做圆周运动,再逆时针做圆周运动,最后从A4点射出,
用B1、B2、R1、R2、T1、T2分别表示在磁场Ⅰ区Ⅱ磁感应强度、轨道半径和周期qvB1=m
①
qvB2=m
②
T1=
=
③
T2=
=
④
设圆形区域的半径为r,如答图所示,已知带电粒子过圆心且垂直A3A4进入Ⅱ区磁场,
连接A1A2,△A1OA2为等边三角形,A2为带电粒子在Ⅱ区磁场中运动轨迹的圆心,
其半径R1=A1A2=OA2=r⑤
圆心角∠A1A2O=60°,
所以粒子在Ⅰ区中的速度偏角φ1为60°,
带电粒子在Ⅰ区磁场中运动的时间为t1=
T1⑥
带电粒子在Ⅱ区磁场中运动轨迹的圆心在OA4的中点,即R=
r ⑦
所以粒子在Ⅱ区中的速度偏角φ2为120°,
在Ⅱ区磁场中运动时间为t2=
T2⑧
带电粒子从射入到射出磁场所用的总时间t=t1+t2⑨
由以上各式可得B1=
⑩B2=
故I区磁感应强度为
;II区磁感应强度为
.
 设粒子的入射速度为v,已知粒子带正电,故它在磁场中先顺时针做圆周运动,再逆时针做圆周运动,最后从A4点射出,
设粒子的入射速度为v,已知粒子带正电,故它在磁场中先顺时针做圆周运动,再逆时针做圆周运动,最后从A4点射出,用B1、B2、R1、R2、T1、T2分别表示在磁场Ⅰ区Ⅱ磁感应强度、轨道半径和周期qvB1=m
| v2 |
| R1 |
qvB2=m
| v2 |
| R2 |
T1=
| 2πR1 |
| v |
| 2πm |
| qB1 |
T2=
| 2πR2 |
| v |
| 2πm |
| qB2 |
设圆形区域的半径为r,如答图所示,已知带电粒子过圆心且垂直A3A4进入Ⅱ区磁场,
连接A1A2,△A1OA2为等边三角形,A2为带电粒子在Ⅱ区磁场中运动轨迹的圆心,
其半径R1=A1A2=OA2=r⑤
圆心角∠A1A2O=60°,
所以粒子在Ⅰ区中的速度偏角φ1为60°,
带电粒子在Ⅰ区磁场中运动的时间为t1=
| 1 |
| 6 |
带电粒子在Ⅱ区磁场中运动轨迹的圆心在OA4的中点,即R=
| 1 |
| 2 |
所以粒子在Ⅱ区中的速度偏角φ2为120°,
在Ⅱ区磁场中运动时间为t2=
| 1 |
| 2 |
带电粒子从射入到射出磁场所用的总时间t=t1+t2⑨
由以上各式可得B1=
| 5 |
| 6 |
| πM |
| qt |
| 5 |
| 3 |
| πM |
| qt |
故I区磁感应强度为
| 5 |
| 6 |
| πM |
| qt |
| 5 |
| 3 |
| πM |
| qt |
点评:带电粒子在磁场中的运动,一般可先确定圆心求出半径,再由洛仑兹力充当向心力及圆的性质求解.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
 (2005?广东)如图所示,在一个圆形区域内,两个方向相反且都垂直于纸面的匀强磁场分布在以直径A2A4为边界的两个半圆形区域Ⅰ、Ⅱ中,A2A4与A1A3的夹角为60°.一质量为m、带电量为+q的粒子以某一速度从Ⅰ区的边缘点A1处沿与A1A3成30°角的方向射入磁场,随后该粒子以垂直于A2A4的方向经过圆心O进入Ⅱ区,最后再从A4处射出磁场.已知该粒子从射入到射出磁场所用的时间为t,求Ⅰ区和Ⅱ区中磁感应强度的大小(忽略粒子重力).
(2005?广东)如图所示,在一个圆形区域内,两个方向相反且都垂直于纸面的匀强磁场分布在以直径A2A4为边界的两个半圆形区域Ⅰ、Ⅱ中,A2A4与A1A3的夹角为60°.一质量为m、带电量为+q的粒子以某一速度从Ⅰ区的边缘点A1处沿与A1A3成30°角的方向射入磁场,随后该粒子以垂直于A2A4的方向经过圆心O进入Ⅱ区,最后再从A4处射出磁场.已知该粒子从射入到射出磁场所用的时间为t,求Ⅰ区和Ⅱ区中磁感应强度的大小(忽略粒子重力). 学校开展研究性学习,某研究性学习小组的同学根据所学的光学知识,设计了一个测量液体折射率的仪器,如图所示.在一个圆形木盘上过其圆心O作两条相互垂直的直径BC、EF,在半径OA上垂直圆盘面插下两枚大头针P1、P2并保持P1、P2的位置不变,每次测量时,让圆盘的BFC部分竖直进入液体中,而且总使得液面与直径BC相平,EF为界面的法线,而后在图中右上方区域观察P1、P2的像,并在圆周上插上大头针P3,使P3正好挡住P1、P2.同学们通过计算,预先在圆周EC部分刻好了折射率的值.这样只要根据P所插的位置,就可直接读出液体折射率的值.则
学校开展研究性学习,某研究性学习小组的同学根据所学的光学知识,设计了一个测量液体折射率的仪器,如图所示.在一个圆形木盘上过其圆心O作两条相互垂直的直径BC、EF,在半径OA上垂直圆盘面插下两枚大头针P1、P2并保持P1、P2的位置不变,每次测量时,让圆盘的BFC部分竖直进入液体中,而且总使得液面与直径BC相平,EF为界面的法线,而后在图中右上方区域观察P1、P2的像,并在圆周上插上大头针P3,使P3正好挡住P1、P2.同学们通过计算,预先在圆周EC部分刻好了折射率的值.这样只要根据P所插的位置,就可直接读出液体折射率的值.则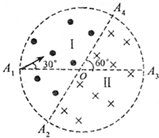 如图所示,在一个圆形区域内,两个方向相反且都垂直于纸面的匀强磁场分布在以直径A2A4为边界的两个半圆形区域Ⅰ、Ⅱ中,A2A4与A1A3的夹角为60°.一质量为m、带电量为+q的粒子以某一速度从Ⅰ区的边缘A1点处沿A1A3成30°角且平行纸面的方向射入磁场,随后该粒子经过圆心O进入Ⅱ区,最后再从A4处射出磁场.则Ⅰ区和Ⅱ区中磁场磁感应强度的大小之比B1:B2为(忽略粒子的重力)( )
如图所示,在一个圆形区域内,两个方向相反且都垂直于纸面的匀强磁场分布在以直径A2A4为边界的两个半圆形区域Ⅰ、Ⅱ中,A2A4与A1A3的夹角为60°.一质量为m、带电量为+q的粒子以某一速度从Ⅰ区的边缘A1点处沿A1A3成30°角且平行纸面的方向射入磁场,随后该粒子经过圆心O进入Ⅱ区,最后再从A4处射出磁场.则Ⅰ区和Ⅱ区中磁场磁感应强度的大小之比B1:B2为(忽略粒子的重力)( )