题目内容
如图所示,地球和某行星在同一轨道平面内同向绕太阳做匀速圆周运动。已知地球的运转周期为T,且行星的轨道半径比地球的轨道半径小,地球和太阳中心的连线与地球和行星的连线所夹的角叫做地球对该行星的观察视角(简称视角)。已知该行星的最大视角为q,当行星处于最大视角处时,是地球上的天文爱好者观察该行星的最佳时期。(1)求行星绕太阳转动的角速度w行与地球绕绕太阳转动的角速度w地的比值w行:w地;
(2)若某时刻该行星正处于最佳观察期,问该行星下一次处于最佳观察期至少需经历多长时间?

(1)要角最大,必须地球与行星的连线与行星的轨道相切,则行星的轨道半径为r=r地sinq,由G=mw2r得:==,(2)若行星原来处于落后于地球的位置,下一次是到超前于地球的位置,则(w行-w地)t=2(-q),t=T,若行星原来处于超前于地球的位置,下一次是到下一周中落后于地球的位置,则(w行-w地)t=2p-[2(-q)],t=T,

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
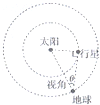 如图所示,某行星绕太阳作匀速圆周运动,其轨道平面和绕行方向均与地球相同地球的公转周期为T行星与地球间的连线与日地连线所成的夹角叫做地球对行星的观察视角当此视角最大时,是在地球上观察该行星的最佳时期已知地球对该行星的最大视角为θ则( )
如图所示,某行星绕太阳作匀速圆周运动,其轨道平面和绕行方向均与地球相同地球的公转周期为T行星与地球间的连线与日地连线所成的夹角叫做地球对行星的观察视角当此视角最大时,是在地球上观察该行星的最佳时期已知地球对该行星的最大视角为θ则( )A、该行星的动行周期为T=
| ||
| B、该行星绕太阳运行的线速度比地球小 | ||
| C、该行星的向心加速度比地球小 | ||
| D、该行星受到太阳的引力比地球受太阳的引力大 |
 (2013?丰台区二模)某卫星的发射过程如图所示,先将卫星从地面发射并从A点进入椭圆轨道I运行,然后在B点通过改变卫星的速度,让卫星进入预定圆形轨道II上运行.则下列说法正确的是( )
(2013?丰台区二模)某卫星的发射过程如图所示,先将卫星从地面发射并从A点进入椭圆轨道I运行,然后在B点通过改变卫星的速度,让卫星进入预定圆形轨道II上运行.则下列说法正确的是( ) 如图所示,天文学家观测到某行星和地球在同一轨道平面内绕太阳做同向匀速圆周运动,且行星的轨道半径比地球的轨道半径小,已知地球的运转周期为T,地球和太阳中心与连线与地球和行星的连线所夹角叫做地球对该行星的观察视角(简称视角),已知该行星的最大视角为θ,当行星处于最大视角处时,是地球上的天文爱好者观察该行星的最佳时期,则行星绕太阳转动的角速度ω行与地球绕太阳转动的角速度ω地的比值ω行:ω地为( )
如图所示,天文学家观测到某行星和地球在同一轨道平面内绕太阳做同向匀速圆周运动,且行星的轨道半径比地球的轨道半径小,已知地球的运转周期为T,地球和太阳中心与连线与地球和行星的连线所夹角叫做地球对该行星的观察视角(简称视角),已知该行星的最大视角为θ,当行星处于最大视角处时,是地球上的天文爱好者观察该行星的最佳时期,则行星绕太阳转动的角速度ω行与地球绕太阳转动的角速度ω地的比值ω行:ω地为( )
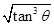 B.
B.
 D.
D.