题目内容
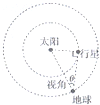如图所示，某行星绕太阳作匀速圆周运动，其轨道平面和绕行方向均与地球相同地球的公转周期为T行星与地球间的连线与日地连线所成的夹角叫做地球对行星的观察视角当此视角最大时，是在地球上观察该行星的最佳时期已知地球对该行星的最大视角为θ则（ ）A、该行星的动行周期为T=
| ||
| B、该行星绕太阳运行的线速度比地球小 | ||
| C、该行星的向心加速度比地球小 | ||
| D、该行星受到太阳的引力比地球受太阳的引力大 |
分析：地球与某行星围绕太阳做匀速圆周运动，根据万有引力提供向心力分别列出等式，解出周期．
解答：解：A、由几何知识可知，当视线与行星轨道相切时视角最大，所以行星轨道半径r=Rsinθ；
设太阳质量为M，地球周期为T，行星周期为T1，
对地球：G
=m（
）2R
对行星：G
=m′（
）2r
联立解之得T1=T
故A正确；
B、根据万有引力提供向心力，有：
G
=m
可得环绕速度：v=
，环绕半径越大，线速度越小，故该行星绕太阳运行的线速度比地球大，故B错误；
C、根据万有引力提供向心力，有：
G
=ma
解得：a=
，环绕半径越大，加速度越小，故该行星的向心加速度比地球大，故C错误；
D、由于不知道该行星的质量与地球质量的关系，故无法比较万有引力大小，故D错误；
故选：A．
设太阳质量为M，地球周期为T，行星周期为T1，
对地球：G
| Mm |
| R2 |
| 2π |
| T |
对行星：G
| Mm′ |
| r2 |
| 2π |
| T1 |
联立解之得T1=T
| sin3θ |
故A正确；
B、根据万有引力提供向心力，有：
G
| Mm |
| R2 |
| v2 |
| R |
可得环绕速度：v=
|
C、根据万有引力提供向心力，有：
G
| Mm |
| R2 |
解得：a=
| GM |
| R2 |
D、由于不知道该行星的质量与地球质量的关系，故无法比较万有引力大小，故D错误；
故选：A．
点评：向心力的公式选取要根据题目提供的已知物理量或要求解的物理量选取应用．要注意物理问题经常要结合数学几何关系解决．正确作图是解题的关键．
练习册系列答案
相关题目
，k是一个对所有行星都相同的常量。将行星绕太阳的运动按圆周运动处理，请你推导出太阳系中该常量k的表达式。已知引力常量为G，太阳的质量为M太。
①
②
③
④
如图所示，在以坐标原点O为圆心、半径为R的半圆形区域内，有相互垂直的匀强电场和匀强磁场，磁感应强度为B，磁场方向垂直于xOy平面向里。一带正电的粒子（不计重力）从O点沿y轴正方向以某一速度射入，带电粒子恰好做匀速直线运动，经t0时间从P点射出。
时间恰从半圆形区域的边界射出。求粒子运动加速度的大小。