题目内容
 如图所示,导线框abcd固定在竖直平面内,bc段的电阻为R,其它电阻均可忽略.Ef是一电阻r的水平放置的导电杆,杆长为l,质量为m,杆的两端分别与ab和cd保持良好接触又能沿它们无摩擦地滑动.整个装置放在磁感应强度为B的匀强磁场中,磁场方向与框面垂直.现用一恒力F向上拉ef,当ef匀速上升时,求:
如图所示,导线框abcd固定在竖直平面内,bc段的电阻为R,其它电阻均可忽略.Ef是一电阻r的水平放置的导电杆,杆长为l,质量为m,杆的两端分别与ab和cd保持良好接触又能沿它们无摩擦地滑动.整个装置放在磁感应强度为B的匀强磁场中,磁场方向与框面垂直.现用一恒力F向上拉ef,当ef匀速上升时,求:(1)导线杆ef受到的安培力的大小
(2)导电杆ef向上运动速度的大小
(3)导电杆ef两端的电压.
分析:(1)对棒受力分析,受重力、拉力和向下的安培力,根据平衡条件求解安培力;
(2)根据安培力公式求解电流,根据闭合电路欧姆定律列式求解电动势,然后根据切割公式求解切割速度;
(3)欧姆定律求解ef两端的电压.
(2)根据安培力公式求解电流,根据闭合电路欧姆定律列式求解电动势,然后根据切割公式求解切割速度;
(3)欧姆定律求解ef两端的电压.
解答:解:(1)对棒受力分析,受重力、拉力和向下的安培力,根据平衡条件,有:
mg+FA=F
解得:FA=F-mg;
(2)根据安培力公式,有:FA=BIL;
根据闭合电路欧姆定律,有:E=I(R+r);
根据切割公式,有:E=BLv;
联立解得:
I=
;
v=
;
(3)ef两端的电压为:U=IR=
;
答:(1)导线杆ef受到的安培力的大小为F-mg;
(2)导电杆ef向上运动速度的大小为
;
(3)导电杆ef两端的电压为
.
mg+FA=F
解得:FA=F-mg;
(2)根据安培力公式,有:FA=BIL;
根据闭合电路欧姆定律,有:E=I(R+r);
根据切割公式,有:E=BLv;
联立解得:
I=
| F-mg |
| BL |
v=
| (F-mg)(R+r) |
| B2L2 |
(3)ef两端的电压为:U=IR=
| (F-mg)R |
| BL |
答:(1)导线杆ef受到的安培力的大小为F-mg;
(2)导电杆ef向上运动速度的大小为
| (F-mg)(R+r) |
| B2L2 |
(3)导电杆ef两端的电压为
| (F-mg)R |
| BL |
点评:本题关键是明确棒的受力情况,然后根据平衡条件求解出安培力;最后根据安培力公式、闭合电路欧姆定律、切割公式列式求解,不难.

练习册系列答案
相关题目
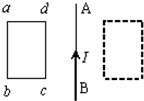 如图所示,导线框abcd与导线AB在同一平面内,直导线中通有恒定的电流I,当线框由左向右匀速通过直导线的过程中,线框中感应电流的方向是( )
如图所示,导线框abcd与导线AB在同一平面内,直导线中通有恒定的电流I,当线框由左向右匀速通过直导线的过程中,线框中感应电流的方向是( )| A、先abcda,再dcbad,后abcda | B、先abcda,再dcbad | C、始终是dcbad | D、先dcbad,再abcda,后dcbad |
 如图所示,导线框abcd置于磁场方向竖直向下的匀强磁场中,可绕MN轴转动,导线框中通以MabcdN方向的恒定电流I后,导线框往纸外偏转θ角而达到平衡,如果改用密度为原来材料1/2的材料做成线框,要使静止时与竖直方向的夹角θ角保持不变,则可以( )
如图所示,导线框abcd置于磁场方向竖直向下的匀强磁场中,可绕MN轴转动,导线框中通以MabcdN方向的恒定电流I后,导线框往纸外偏转θ角而达到平衡,如果改用密度为原来材料1/2的材料做成线框,要使静止时与竖直方向的夹角θ角保持不变,则可以( ) 如图所示,导线框abcd与固定直导线AB在同一平面内,直导线AB中通有恒定电流I,当线框由图示位置向右匀速运动的过程中( )
如图所示,导线框abcd与固定直导线AB在同一平面内,直导线AB中通有恒定电流I,当线框由图示位置向右匀速运动的过程中( )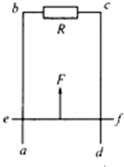 如图所示,导线框abcd固定在竖直平面内,导线ab和cd间的宽度为l,bc间电阻阻值为R,其它电阻均可忽略.ef是一电阻可忽略的水平放置的导体杆,杆的质量为m,杆的两端分别与ab和cd保持良好接触,且能沿导线框无摩擦地滑动,磁感应强度为B的匀强磁场方向与框面垂直.现用一恒力F竖直向上拉ef,使其由静止开始运动,当ef上升高度为h时,ef恰好做匀速运动.求:
如图所示,导线框abcd固定在竖直平面内,导线ab和cd间的宽度为l,bc间电阻阻值为R,其它电阻均可忽略.ef是一电阻可忽略的水平放置的导体杆,杆的质量为m,杆的两端分别与ab和cd保持良好接触,且能沿导线框无摩擦地滑动,磁感应强度为B的匀强磁场方向与框面垂直.现用一恒力F竖直向上拉ef,使其由静止开始运动,当ef上升高度为h时,ef恰好做匀速运动.求: