题目内容
【题目】如图所示为固定在竖直平面内的,内壁光滑的绝缘轨道,其半径为R=1m,轨道所在的空间存在平行于轨道的水平向右的匀强电场,场强为E=3×104N/C。在轨道的最下端A处有一个电荷量为q=+2×10-4C、质量为m=0.8kg的小球。现给小球一个水平向右的初速度v0=4m/s,g取10m/s2,则(结果可以用根式表示)
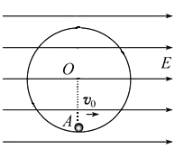
(1)小球运动的最大速度是多少?
(2)要使小球在运动过程中不脱离轨道,其初速度v0要满足什么条件?
(3)取A点所在平面为重力势能的零势能面,在小球能够做完整圆周运动的前提下,求小球运动过程中的最小机械能的大小。
【答案】(1) ![]() (2)
(2) ![]() (3)
(3) ![]()
【解析】
(1)当小球在等效最低点时,速度最大,设小球的最大速度为V,由动能定理
![]()
解得:
![]()
(2)设小球的临界速度为Vm,第一种情况:
![]() ①
①
![]() ②
②
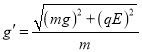 ③
③
由①② ③三式联立得
![]()
第二种情况:
![]()
得
![]()
(3)设最小机械能为Em ,电势能增加最大时,机械能最小
![]()
![]()
代入数据解得:
![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】可见光的波长的大致范围是400~760nm。右表给出了几种金属发生光电效应的极限波长,下列说法正确的是( )
金属 | 钨 | 钙 | 钠 | 钾 |
极限波长 (nm) | 274 | 388 | 542 | 551 |
A.表中所列金属,钾的逸出功最大
B.只要光照时间足够长或强度足够大,所有波长的可见光都可以使钠发生光电效应
C.用波长760nm的光照射金属钠、钾,则钠逸出的光电子最大初动能较大
D.用波长400nm的光照射金属钠、钾,则钾逸出的光电子最大初动能较大