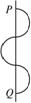题目内容
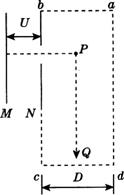
如图所示,一个初速度为零的带正电的粒子经过MN两平行板间电场加速后,从N板上的孔射出,当带电粒子到达P点时,长方形abcd的区域内开始加一大小不变、方向垂直于纸面且方向交替变化的匀强磁场,磁感应强度B=0.4T.每经过 s,磁场方向变化一次,且当粒子到达P点时磁场的方向指向纸外.在Q处有一静止的中性粒子,PQ间距离s=3.0m,PQ直线垂直平分ab、cd.已知长方形abcd区域的宽度D=1.6m,带电粒子的荷质比
s,磁场方向变化一次,且当粒子到达P点时磁场的方向指向纸外.在Q处有一静止的中性粒子,PQ间距离s=3.0m,PQ直线垂直平分ab、cd.已知长方形abcd区域的宽度D=1.6m,带电粒子的荷质比 =1.0×104C/kg,不计重力.
=1.0×104C/kg,不计重力.(1)试通过计算说明,当加速电压为U=200V时,带电粒子能否与中性粒子碰撞?
(2)要使该带电粒子能与位于Q处的中性粒子的碰撞,试求加速电压的最大值Umax.

【答案】分析:(1)洛伦兹力提供向心力,根据牛顿第二定律,推导出周期公式,并由动能定理求出速度,最后由半径公式来确定能否与中性粒子碰撞;
(2)根据长度的关系,来确定相碰条件,从而求得最小半径,由半径公式与动能定理,共同求出加速电压.
解答:解:设带电粒子经电场加速后的速度为v,有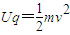 …①
…①
设带电粒子在磁场中运动的周期为T,有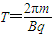 …②
…②
代入数据得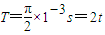 …③
…③
即磁场改变一次方向,粒子正好运动半个周期.
设带电粒子在磁场中运动的半径为r,有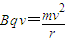 …④
…④
联立得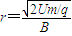 …⑤
…⑤
代入数据得 r=0.5m…⑥
由于 s=3.0m=6r,所以带电粒子能与中性粒子相碰…⑦
(2)要使它们相撞,必须满足s=2nr=3m,且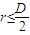 =0.8m.
=0.8m.
显然,当n=2时,r的值符合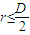 式且最大
式且最大
即 rmax=0.75m… ⑧
得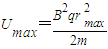 …⑨
…⑨
代入数据得 Umax=450V…⑩
答:(1)如果加速电压U=200V,带电粒子能与中性粒子碰撞;
(2)能使带电粒子与中性粒子碰撞,加速电压的最大值是450V.
点评:考查粒子在磁场中做匀速圆周运动,由洛伦兹力提供向心力,根据牛顿第二定律,推导出的半径与周期公式,并掌握动能定理在此应用,同时还掌握几何关系的运用.
(2)根据长度的关系,来确定相碰条件,从而求得最小半径,由半径公式与动能定理,共同求出加速电压.
解答:解:设带电粒子经电场加速后的速度为v,有
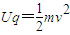 …①
…①设带电粒子在磁场中运动的周期为T,有
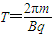 …②
…②代入数据得
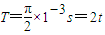 …③
…③即磁场改变一次方向,粒子正好运动半个周期.
设带电粒子在磁场中运动的半径为r,有
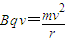 …④
…④联立得
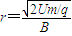 …⑤
…⑤代入数据得 r=0.5m…⑥
由于 s=3.0m=6r,所以带电粒子能与中性粒子相碰…⑦
(2)要使它们相撞,必须满足s=2nr=3m,且
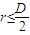 =0.8m.
=0.8m.显然,当n=2时,r的值符合
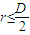 式且最大
式且最大即 rmax=0.75m… ⑧
得
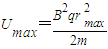 …⑨
…⑨代入数据得 Umax=450V…⑩
答:(1)如果加速电压U=200V,带电粒子能与中性粒子碰撞;
(2)能使带电粒子与中性粒子碰撞,加速电压的最大值是450V.
点评:考查粒子在磁场中做匀速圆周运动,由洛伦兹力提供向心力,根据牛顿第二定律,推导出的半径与周期公式,并掌握动能定理在此应用,同时还掌握几何关系的运用.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 如图所示,一个初速度为零的带正电的粒子经过MN两平行板间电场加速后,从N板上的孔射出,当带电粒子到达P点时,长方形abcd的区域内开始加一大小不变、方向垂直于纸面且方向交替变化的匀强磁场,磁感应强度B=0.4T.每经过
如图所示,一个初速度为零的带正电的粒子经过MN两平行板间电场加速后,从N板上的孔射出,当带电粒子到达P点时,长方形abcd的区域内开始加一大小不变、方向垂直于纸面且方向交替变化的匀强磁场,磁感应强度B=0.4T.每经过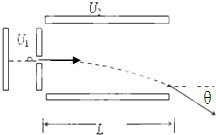 如图所示,一个初速度为零的带电粒子经电压U1的加速电场加速后,沿垂直于偏转电场的场强方向进入偏转电场.已知偏转电场两平行板间的电势差为U2,极板长为L,两板间的距离为d,带电粒子通过偏转电场时的偏转角为θ.试证明:tanθ=
如图所示,一个初速度为零的带电粒子经电压U1的加速电场加速后,沿垂直于偏转电场的场强方向进入偏转电场.已知偏转电场两平行板间的电势差为U2,极板长为L,两板间的距离为d,带电粒子通过偏转电场时的偏转角为θ.试证明:tanθ=