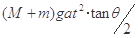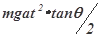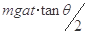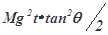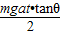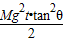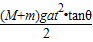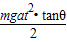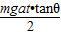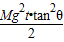题目内容
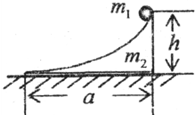 在光滑的水平地面上静止着一个斜面体,其质量为m2,斜面是一个光滑的曲面,斜面体高为h,底边长为a,如图所示.今有一个质量为m1,(m2=nm1)的小球从斜面体的顶端自静止开始下滑,小球滑离斜面体的下端时速度在水平方向,则下列说法正确的是( )
在光滑的水平地面上静止着一个斜面体,其质量为m2,斜面是一个光滑的曲面,斜面体高为h,底边长为a,如图所示.今有一个质量为m1,(m2=nm1)的小球从斜面体的顶端自静止开始下滑,小球滑离斜面体的下端时速度在水平方向,则下列说法正确的是( )| A、小球在下滑中,两者的动量总是大小相等方向相反 | ||||||||
B、两者分开时斜面体向左移动的距离是
| ||||||||
C、分开时小球和斜面体的速度大小分别是
| ||||||||
D、小球在下滑中斜面体弹力对它做的功为
|
分析:小球下滑过程中,系统水平方向不受外力,水平方向动量守恒;要使小球能与弧形槽发生第二次作用,小球从光滑弧形槽滑下量的速度应大于槽的速度,根据系统水平方向动量守恒和机械能守恒求解.
解答:解:
A、对于小球和斜面体组成的系统,由于水平方向不受外力,所以系统水平方向动量守恒,而不是其他方向也守恒,故A错误.
B、至于各自的位移,由于两者共同走完a的路程,故(v1+v2)t=a,得t=
.这样得斜面体的位移s2=
方向向右,而s1=
,得B错误.
C、由于系统水平方向动量守恒,则m1v1-m2v2=0,得v1=nv2.又由于系统没有能量损失,所以系统机械能守恒,即m1gh=
m1v12+
m2v22,结合速度关系得v1=
,
v2=
;故C正确.
D、至于弹力对小球所做的功,由动能定理得m1gh+W=
m1v12,得弹力的功为W=
m1v12-m1gh=-
,故D错误.
故选:C
A、对于小球和斜面体组成的系统,由于水平方向不受外力,所以系统水平方向动量守恒,而不是其他方向也守恒,故A错误.
B、至于各自的位移,由于两者共同走完a的路程,故(v1+v2)t=a,得t=
| a |
| (n+1)v2 |
| a |
| n+1 |
| na |
| n+1 |
C、由于系统水平方向动量守恒,则m1v1-m2v2=0,得v1=nv2.又由于系统没有能量损失,所以系统机械能守恒,即m1gh=
| 1 |
| 2 |
| 1 |
| 2 |
|
v2=
|
D、至于弹力对小球所做的功,由动能定理得m1gh+W=
| 1 |
| 2 |
| 1 |
| 2 |
| m1gh |
| n+1 |
故选:C
点评:本题关键要掌握小球下滑过程中,水平方向不受外力,由动量守恒进行分析.

练习册系列答案
相关题目
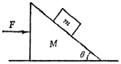
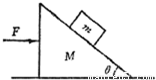
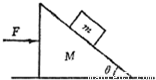
 在光滑的水平地面上静置一个质量为M倾角为θ的斜劈,在斜劈上有一个质量为m的光滑物块,现用水平推力推动斜劈水平向右运动,并使物块与斜劈始终保持相对静止,如图所示,下列叙述中正确的是( )
在光滑的水平地面上静置一个质量为M倾角为θ的斜劈,在斜劈上有一个质量为m的光滑物块,现用水平推力推动斜劈水平向右运动,并使物块与斜劈始终保持相对静止,如图所示,下列叙述中正确的是( )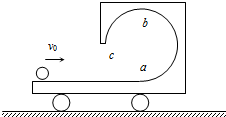
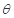 的斜劈,在斜劈上有一个质量为m的光滑物块,现用水平推力推动斜劈水平向右运动,并使物块与斜劈始终保持相对静止,如下图所示,下列叙述中正确的是( )
的斜劈,在斜劈上有一个质量为m的光滑物块,现用水平推力推动斜劈水平向右运动,并使物块与斜劈始终保持相对静止,如下图所示,下列叙述中正确的是( )