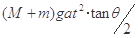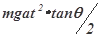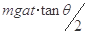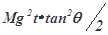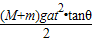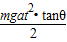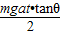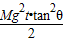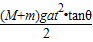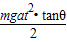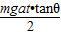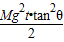题目内容
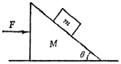
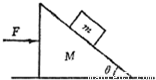
 在光滑的水平地面上静置一个质量为M倾角为θ的斜劈,在斜劈上有一个质量为m的光滑物块,现用水平推力推动斜劈水平向右运动,并使物块与斜劈始终保持相对静止,如图所示,下列叙述中正确的是( )
在光滑的水平地面上静置一个质量为M倾角为θ的斜劈,在斜劈上有一个质量为m的光滑物块,现用水平推力推动斜劈水平向右运动,并使物块与斜劈始终保持相对静止,如图所示,下列叙述中正确的是( )分析:由于物体一起运动,所以它们由共同的加速度,对m受力分析可以求共同的加速度的大小,再由匀变速直线运动的公式可以求的物体的位移和速度的大小,进而可以根据功的公式来计算各个力对物体做功的大小.
解答:解:对物块做受力分析,
因为木块与物块保持物块相对斜面静止,且物块与斜面的接触是光滑的,
所以物块在重力和斜面对物体的斜向上的支持力的共同作用下做加速度运动,设这个加速度为a,所受合力为F′.
由力的分解不难算出 F′=mgtanθ=ma 即a=gtanθ,
将木块与物块看成是一个整体,它们的共同的加速度即为a.
对于整体
则有水平力F=(M+m)a
解得F=(M+m)gtanθ
斜劈起动t秒内,位移的大小是x=
at2 =
gtanθt2,
推力F对斜劈做的功是W=Fx=(M+m)gtanθ?
at2=
,所以A正确.
斜劈起动t秒内,速度的大小是V=at,
对于物体,只有斜劈对物块的弹力做功,由动能定理可得,
W=
mV2=
m(at)2=
mgtanθat2,所以B正确.
由于物体的重力不做功,所以合力的功率即为斜劈对物块的弹力的功率,
所以P=
=
mgtanθat,所以C正确.
在斜劈起动t秒末,合力对斜劈的即时功率为P′=FV=(M+m)gtanθ?at=(M+m)(gtanθ)2t,所以D错误.
故选ABC.
因为木块与物块保持物块相对斜面静止,且物块与斜面的接触是光滑的,
所以物块在重力和斜面对物体的斜向上的支持力的共同作用下做加速度运动,设这个加速度为a,所受合力为F′.
由力的分解不难算出 F′=mgtanθ=ma 即a=gtanθ,
将木块与物块看成是一个整体,它们的共同的加速度即为a.
对于整体
则有水平力F=(M+m)a
解得F=(M+m)gtanθ
斜劈起动t秒内,位移的大小是x=
| 1 |
| 2 |
| 1 |
| 2 |
推力F对斜劈做的功是W=Fx=(M+m)gtanθ?
| 1 |
| 2 |
| (M+m)gat2?tanθ |
| 2 |
斜劈起动t秒内,速度的大小是V=at,
对于物体,只有斜劈对物块的弹力做功,由动能定理可得,
W=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
由于物体的重力不做功,所以合力的功率即为斜劈对物块的弹力的功率,
所以P=
| W |
| t |
| 1 |
| 2 |
在斜劈起动t秒末,合力对斜劈的即时功率为P′=FV=(M+m)gtanθ?at=(M+m)(gtanθ)2t,所以D错误.
故选ABC.
点评:当遇到多个物体共同运动时,通常可以采用整体法和隔离法,通过整体法可以求得系统的加速度的大小,再由隔离法可以求得物体的受力等情况.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案
相关题目
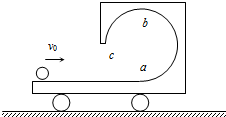
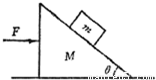
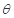 的斜劈,在斜劈上有一个质量为m的光滑物块,现用水平推力推动斜劈水平向右运动,并使物块与斜劈始终保持相对静止,如下图所示,下列叙述中正确的是( )
的斜劈,在斜劈上有一个质量为m的光滑物块,现用水平推力推动斜劈水平向右运动,并使物块与斜劈始终保持相对静止,如下图所示,下列叙述中正确的是( )