题目内容
 在竖直向下的匀强电场中有一带负电的小球,自绝缘斜面的A点由静止开始滑下,接着通过绝缘的离心轨道的最高点B.已知小球的质量为m,带电荷量为大小q,圆弧轨道半径为R,匀强电场场强为E,且mg>Eq,运动中摩擦阻力及空气阻力不计,求:
在竖直向下的匀强电场中有一带负电的小球,自绝缘斜面的A点由静止开始滑下,接着通过绝缘的离心轨道的最高点B.已知小球的质量为m,带电荷量为大小q,圆弧轨道半径为R,匀强电场场强为E,且mg>Eq,运动中摩擦阻力及空气阻力不计,求:(1)A点距地面的高度h至少应为多少?
(2)当h取最小值时,小球对最低点C的压力为多少?
分析:(1)根据重力与电场力的合力提供向心力,结合牛顿第二定律与动能定理,即可求解;
(2)根据受力分析,由牛顿第二定律与动能定理,即可求解人.
(2)根据受力分析,由牛顿第二定律与动能定理,即可求解人.
解答:解:(1)由分析知,小球要经过B点至少需满足条件重力与电场力的合力提供向心力,
即 mg-qE=
①
又从A到B过程由动能定理得:(mg-qE)(h-2R)=
②
解①②得:h=2.5R
(2)在C点,对小球受力分析得:FN-(mg-qE)=
③
从A到C过程由动能定理得:(mg-qE)h=
④
解③④得:FN=(mg-qE)+
=6(mg-qE)
由牛顿第三定律知,小球对C点的压力与轨道在C点给小球的支持力是一对相互作用力,所以小球对C点的压力为6(mg-Eq).
答:(1)A点距地面的高度h至少应为2.5R;
(2)当h取最小值时,小球对最低点C的压力为6(mg-Eq).
即 mg-qE=
m
| ||
| R |
又从A到B过程由动能定理得:(mg-qE)(h-2R)=
m
| ||
| R |
解①②得:h=2.5R
(2)在C点,对小球受力分析得:FN-(mg-qE)=
m
| ||
| R |
从A到C过程由动能定理得:(mg-qE)h=
m
| ||
| 2 |
解③④得:FN=(mg-qE)+
| 2(mg-qE)h |
| R |
由牛顿第三定律知,小球对C点的压力与轨道在C点给小球的支持力是一对相互作用力,所以小球对C点的压力为6(mg-Eq).
答:(1)A点距地面的高度h至少应为2.5R;
(2)当h取最小值时,小球对最低点C的压力为6(mg-Eq).
点评:考查牛顿第二定律与动能定理的应用,掌握受力分析的方法,理解提供向心力的来源,注意电场力做负功.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 在竖直向下的匀强电场中,有a、b、c、d四个带电小球.各以水平向左、水平向右、竖直向下和竖直向上的速度做匀速直线运动,不计小球间的相互作用力,则有( )
在竖直向下的匀强电场中,有a、b、c、d四个带电小球.各以水平向左、水平向右、竖直向下和竖直向上的速度做匀速直线运动,不计小球间的相互作用力,则有( )| A、c、d带异种电荷 | B、a、b带同种电荷且电势能均不变 | C、d的电势能减小,重力势能增加 | D、c的电势能减小,重力势能增加 |
 如图所示,在竖直向下的匀强电场中有一绝缘的光滑离心轨道,一个带负电的小球从斜轨道上的A点由静止释放,沿轨道滑下,已知小球的质量为m,电量大小为-q,匀强电场的场强大小为E,斜轨道的倾角为α (小球的重力大于所受的电场力).
如图所示,在竖直向下的匀强电场中有一绝缘的光滑离心轨道,一个带负电的小球从斜轨道上的A点由静止释放,沿轨道滑下,已知小球的质量为m,电量大小为-q,匀强电场的场强大小为E,斜轨道的倾角为α (小球的重力大于所受的电场力).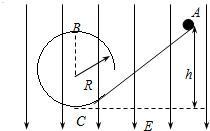 如图所示,在竖直向下的匀强电场中,一个质量为m带负电的小球从斜轨道上的A点由静止滑下,小球通过半径为R的圆轨道顶端的B点时恰好不落下来.已知轨道是光滑而又绝缘的,且小球的重力是它所受的电场力2倍.求:
如图所示,在竖直向下的匀强电场中,一个质量为m带负电的小球从斜轨道上的A点由静止滑下,小球通过半径为R的圆轨道顶端的B点时恰好不落下来.已知轨道是光滑而又绝缘的,且小球的重力是它所受的电场力2倍.求: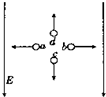 如图在竖直向下的匀强电场中,有a、b、c、d四个带电质点,各以水平向左、水平向右、竖直向下和竖直向上的速度做匀速直线运动,不计质点间的相互作用力,则下面说法不正确是( )
如图在竖直向下的匀强电场中,有a、b、c、d四个带电质点,各以水平向左、水平向右、竖直向下和竖直向上的速度做匀速直线运动,不计质点间的相互作用力,则下面说法不正确是( )