题目内容
货车A正在该公路上以20m/s的速度匀速行驶,。因疲劳驾驶司机注意力不集中,当司机发现正前方有一辆静止的轿车B时,两车距离仅有76m。
(1)若此时B车立即以2m/s2的加速度启动,通过计算判断:如果A车司机没有刹车,是否会撞上B车;若不相撞,求两车相距最近时的距离;若能,从A车发现B车开始到撞上B车的时间?
(2)若A车司机发现B车立即刹车(不计反应时间)做匀减速直线运动,加速度大小为2m/s2(两车均视为质点),为了避免碰撞,A车在刹车同时,向B车发出信号,B车收到信号,经△t=2s的反应时间才开始匀加速向前行驶,问:B车加速度a2至少多大才能避免事故?(这段公路很窄,无法靠边让道)
(1)会  s, (2)a
s, (2)a 1.2m/s2
1.2m/s2
【解析】
试题分析:已知:L=76m,v=20m/s,a=2m/s2
(1)当两车速度相等时,所要的时间t0= =10s,
=10s,
在这10s内,A车的位移xA=vt0=200m
B车的位移xB= =100m;因为xA=200M> xB+L=100m+76m,所以会撞上。
=100m;因为xA=200M> xB+L=100m+76m,所以会撞上。
设经过时间t两车相撞,有:vt- =L,代入数值解得:t=
=L,代入数值解得:t= s(另一根舍去)
s(另一根舍去)
(2)已知A车的加速度a1=-2m/s2,初速度v=20m/s,△t=2s。设B车的加速度为a2,B车运动后后当经过时间t,两车相遇。B车的运动时间为t,A车的运动时间为t+△t,则有:
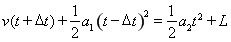
要以免碰撞,则t 无实根,解得)a 1.2m/s2
1.2m/s2
考点:匀变速直线运动的速度与时间的关系;匀变速直线运动的位移与时间的关系

 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案汽车起动的快慢和能够达到的最大速度,是衡量汽车性能的指标体系中的两个重要指标。汽车起动的快慢用车的速度从0到100km/h的加速时间来表示,这个时间越短,汽车起动的加速度就越大。下表中列出了两种汽车的性能指标(为了简化计算,把100km/h取为30m/s)。
| 起动的快慢(单位:s) (0~30m/s的加速时间) | 最大速度(m/s) |
甲车 | 12 | 40 |
乙车 | 6 | 50 |
现在,甲、乙两车在同一条平直公路上,车头向着同一个方向,乙车在前,甲车在后,两车相距200m,甲车先起动,经过一段时间乙车再起动。若两车从速度为0到最大速度的时间内都以最大加速度起动做匀加速直线运动(达最大速度后做匀速运动),若在乙车开出8s时两车相遇,则:
(1)甲、乙两车的起动加速度分别是多少?
(2)相遇时乙车发生的位移是多少?
(3)甲车比乙车提前运动的时间为多少?



