题目内容
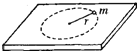
【题目】在无风的羽毛球馆中,某人在离地面高为H处,将质量为m的羽毛球以速度![]() 水平击出,假设羽毛球在空气中运动时所受的阻力
水平击出,假设羽毛球在空气中运动时所受的阻力![]() ,其中
,其中![]() 是球的速度,k是已知的常数,阻力的方向与速度方向相反,并且球在着地前已经竖直向下做匀速运动,重力加速度为g。求:
是球的速度,k是已知的常数,阻力的方向与速度方向相反,并且球在着地前已经竖直向下做匀速运动,重力加速度为g。求:
(1)羽毛球刚被击出时加速度的大小;
(2)求羽毛球从被击出到着地过程中克服空气阻力做的功W;
(3)若另有一个与上述相同的羽毛球从同一地点由静止释故,并且球在着地前也以作匀速运动,试比较两球落地所需时间和着地时的速度,并简述理由。
【答案】解:(1)小球刚抛出时受到的合力F=![]() ,由牛顿第二定律,F=ma,
,由牛顿第二定律,F=ma,
解得小球刚抛出时加速度大小a=![]() /m。
/m。
(2)球最终竖直向下做匀速直线运动,设此时速度为v,则mg=kv。
设球从抛出到着地过程中克服空气阻力做的功为W,由动能定理有,mgH-W=![]() mv2-
mv2-![]() mv02,
mv02,
解得:W=mgH+![]() mv02-
mv02-![]() 。
。
(3)根据运动的独立性,在竖直方向都是从静止开始的运动,受到的合力均为Fy=mg-kvy,加速度均为ay="g-" kvy/m。故在竖直方向的运动是相同的,运动时间相等,着地时速度都是v=mg/k。
【解析】应用牛顿第二定律、动能定理及其相关知识列方程解答。

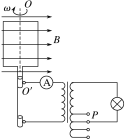
【题目】如图甲所示为测量电动机转动角速度的实验装置,半径不大的圆形卡纸固定在电动机转轴上,在电动机的带动下匀速转动.在圆形卡纸的旁边安装一个改装了的电火花计时器。
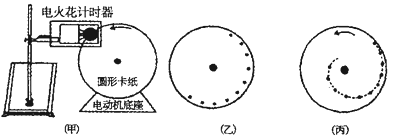
下面是该实验的实验步骤:
①使电火花计时器与圆形卡纸保持良好接触;
②启动电动机,使圆形卡纸转动起来;
③接通电火花计时器的电源,使它工作起来;
④关闭电动机,拆除电火花计时器;研究卡纸上留下的一段痕迹(如图乙所示),写出角速度ω的表达式,代入数据,得出ω的测量值。
(1)要得到角速度ω的测量值,还缺少一种必要的测量工具,它是________
A.秒表 | B.游标卡尺 | C.圆规 | D.量角器 |
(2)设电火花计时器打点时间间隔为t,卡纸上有连续打下的n个点,写出ω的表达式,并指出表达式中各个物理量的含义__________________;
(3)为了避免在卡纸连续转动的过程中出现打点重叠,在电火花计时器与盘面保持良好接触的同时,可以缓慢地将电火花计时器沿圆形卡纸半径方向向卡纸中心移动。则卡纸上打下的点的分布曲线不是一个圆,而是类似一种螺旋线,如图丙所示。你认为这对测量结果有无影响,写出理由_____________________