题目内容
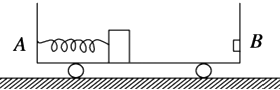
【题目】如图所示，水平面上有两个木块，两木块的质量分别为m1、m2 ， 且m2=2m1 ． 开始两木块之间有一根用轻绳缚住的已压缩的轻弹簧，烧断细绳后，两木块分别向左、右运动．若两木块m1和m2与水平面间的动摩擦因数为μ1、μ2 ， 且μ1=2μ2 ， 则在弹簧伸长的过程中，两木块（ ）
A.动量大小之比为1：1
B.速度大小之比为2：1
C.通过的路程之比为2：1
D.通过的路程之比为1：1
【答案】A,B,C
【解析】解：以两木块及弹簧为研究对象，绳断开后，弹簧将对两木块有推力作用，这可以看成是内力；
水平面对两木块有方向相反的滑动摩擦力，且F1=μ1m1g，F2=μ2m2g，系统所受合外力F合=μ1m1g﹣μ2m2g=0，系统动量守恒；
设弹簧伸长过程中某一时刻，两木块速度大小分别为v1、v2，以向右为正方向，由动量守恒定律得：﹣m1v1+m2v2=0，即m1v1=m2v2，
A、两物体的动量大小之比为1：1，故A正确．
B、两物体的速度大小之比： 
= 
= 
，故B正确．
C、弹簧伸长过程中，两木块的运动时间相等，任意时刻速度之比为2：1，则两木块通过的路程之比： 
= 
= = ，故C正确，D错误．
故选：ABC．
系统所受合外力为零，系统动量守恒，根据动量守恒条件判断系统动量是否守恒，然后应用动量守恒定律分析答题．
练习册系列答案
相关题目
