如图所示.一质量为m带正电的小球.用长为L的绝缘细线悬挂于O点.处于一水平方向的匀强电场中.静止时细线右偏与竖直方向成45°角.位于图中的P点．重力加速度为g.求:(1)静止在P点时线的拉力是多大?(2)如将小球向右拉紧至与O点等高的A点由静止释放.则当小球摆至P点时.其电势能如何变?变化了多少?(3) 如将小球向左拉紧至与O点等高的B点由静止释放.则小球到达P点时题目和参考答案——青夏教育精英家教网—

题目内容

（12分）如图所示，一质量为m带正电的小球，用长为L的绝缘细线悬挂于O点，处于一水平方向的匀强电场中，静止时细线右偏与竖直方向成45°角，位于图中的P点．重力加速度为g，求：

（1）静止在P点时线的拉力是多大？
（2）如将小球向右拉紧至与O点等高的A点由静止释放，则当小球摆至P点时，其电势能如何变？变化了多少？
（3）如将小球向左拉紧至与O点等高的B点由静止释放，则小球到达P点时的速度大小？

（1）T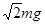＝（2）其电势能增加为（3）v_C^′＝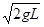

解析试题分析：（1）小球静止在P点时由平衡条件得           1分
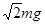解得：T＝           1分
（2）小球从A到P的过程中，电场力F做负功，故其电势能增加  [来源:学_科_网]
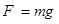由（1）问得，故              1分
则小球克服电场力做功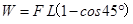              2分
其电势能增加为         1分
（3）小球先做匀加速直线运动到达最低点C，
根据动能定理得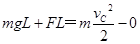：           1分
解得：v_C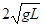＝          1分
到达C点后细绳绷紧，小球沿细绳方向的速度变为零，则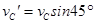
解得：v_C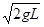^′＝               1分
从C到P做圆周运动，由动能定理得：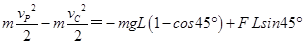
          2分
解得v_P＝         1分
考点：考查了共点力平衡条件，功能关系，动能定理，运动的合成与分解

练习册系列答案

相关题目

（8分）某研究性学习小组在探究电荷间的相互作用与哪些因素有关时，设计了以下实验：
（1）该组同学首先将一个带正电的球体A固定在水平绝缘支座上。把系在绝缘细线上的带正电的小球B（图中未画出）先后挂在图中P₁、P₂、P₃位置，比较小球在不同位置所受带电体的作用力的大小。同学们根据力学知识分析得出细线偏离竖直方向的角度越小，小球B所受带电球体A的作用力          （填“越大”或“越小”或“不变”），实验发现小球B在位置      细线偏离竖直方向的角度最大（填“P₁或P₂或P₃”）

（2）接着该组同学使小球处于同一位置，增大或减少小球A所带的电荷量，比较小球所受作用力大小的变化。如图，悬挂在P₁点的不可伸长的绝缘细线下端有一个带电量不变的小球B。在两次实验中，均缓慢移动另一带同种电荷的小球A。当A球到达悬点P₁的正下方并与B在同一水平线上B处于受力平衡时，悬线偏离竖直方向角度为θ。若两次实验中A的电量分别为q₁和q₂，θ分别为30°和45°，则q₂/q₁为（    ）
A．2          B．3           C．         D．

如图所示，物体A的质量m_A＝0.2kg，放在水平面上的物体B的质量m_B＝1.0kg，绳和滑轮间的摩擦及质量均不计，且绳的OB部分水平，OA部分竖直，A和B恰好一起匀速运动。（g＝10m/s²）求：
（1）物体B与桌面间的动摩擦因数？
（2）如果用水平力F向左拉B，使物体A和B做匀速运动，需多大的拉力？
（3）若在原来静止的物体B上放一个质量与B物体质量相等的物体后，物体B受到的摩擦力多大？

如图所示，空间有场强E=1.0×10²V/m竖直向下的电场，长L=0.8m不可伸长的轻绳固定于O点．另一端系一质量m=0.5kg带电q=5×10^-2C的小球．拉起小球至绳水平后在A点无初速度释放，当小球运动至O点的正下方B点时绳恰好断裂，小球继续运动并垂直打在同一竖直平面且与水平面成θ=53°、无限大的挡板MN上的C点．试求：

（1）绳子的最大张力；
（2）A、C两点的电势差；
（3）当小球运动至C点时，突然施加一恒力F作用在小球上，同时把挡板迅速水平向右移至某处，若小球仍能垂直打在档板上，所加恒力F的方向及取值范围．

如图所示，倾角为θ＝30°的光滑导体滑轨A和B，上端接入一电动势E＝3V、内阻不计的电源，滑轨间距为L＝0.1m，将一个质量为m＝0.03 kg，电阻R＝0.5Ω的金属棒水平放置在滑轨上，若滑轨周围存在着垂直于滑轨平面的匀强磁场，当闭合开关S后，金属棒刚好静止在滑轨上，求滑轨周围空间的磁场方向和磁感应强度的大小．(重力加速度取g＝10 m/s²)

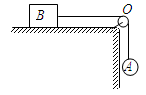
（10分）如图所示，通电金属杆ab质量m=12g,电阻R=1.5Ω，水平地放置在倾角θ=30⁰的光滑金属导轨上。导轨宽度,导轨电阻、导轨与金属杆的接触电阻忽略不计，电源内阻r=0.5Ω。匀强磁场的方向竖直向上，磁感应强度B=0.2T。g=10若金属棒ab恰能保持静止,求：

（1）金属杆ab受到的安培力大小；
（2）电源的电动势大小E。

（16分）如图所示，固定在竖直平面的光滑绝缘圆环处于匀强电场中，场强方向与圆环平面平行且与水平方向成30°，环上与圆心O等高的A点套有一个质量为m，电荷量为+q的小球恰好处于平衡状态．（重力加速度为g），求：

（1）匀强电场的场强大小
（2）某时刻突然将电场方向变为竖直向下，场强大小不变，小球滑到最低点B时对环的压力大小

（10分）如图所示，在匀强磁场中倾斜放置两根平行金属导轨，导轨与水平面夹角为，磁场方向垂直导轨平面向下，磁感应强度的大小为B，平行导轨间距为L。两根金属杆ab和cd可以在导轨上无摩擦地滑动。两金属杆的质量均为m，电阻均为R，导轨的电阻不计。若用与导轨平面平行的拉力F作用在金属杆ab上，使ab匀速上滑，cd杆在导轨上恰好保持静止。求

（1）拉力F的大小，
（2）ab杆上滑的速度大小。

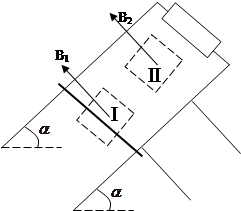
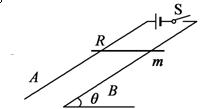
（14分）如图所示，倾角为的光滑导轨上端接入一定值电阻，Ⅰ和Ⅱ是边长都为L的两正方形磁场区域，其区域内的磁场方向都垂直于导轨平面向上，区域Ⅰ中磁场的磁感强度为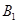，区域Ⅱ中磁场随时间按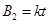变化，一质量为、电阻为的金属杆穿过区域Ⅰ垂直地跨放在两导轨上，并恰能保存静止。试求：

（1）通过金属杆的电流大小;
（2）定值电阻的阻值为多大？

试题分类