题目内容
6.先后让一束质子(${\;}_{1}^{1}$H)和一束α粒子(${\;}_{2}^{4}$He)通过同一对平行金属板形成的偏转电场,已知板长为L,板间距为d,粒子进入时速度方向与板平行.求:(1)质子和α粒子以相同的初速度v0射入时的侧向偏移量之比;
(2)质子和α粒子以相同的初动能射入时的偏转角度正切值之比.
分析 (1)粒子在偏转电场中做类平抛运动,由牛顿第二定律求得加速度;粒子垂直于电场方向做匀速直线运动,平行于电场方向做初速度为零的匀加速运动,由运动学公式求出侧移量的表达式,结合两个粒子的比荷,进行求解.
(2)粒子垂直于电场方向做匀速直线运动,平行于电场方向做初速度为零的匀加速运动,由运动学公式求出偏角的正切表达式,结合两个粒子的比荷,进行求解.
解答 解:(1)粒子做类似平抛运动,加速度为:
a=$\frac{qE}{m}$
根据分位移公式,有:
L=v0t
$y=\frac{1}{2}a{t}^{2}$
联立解得:
y=$\frac{qE{L}^{2}}{2m{v}_{0}^{2}}$
质子(${\;}_{1}^{1}$H)和α粒子(${\;}_{2}^{4}$He)的初速度相同,故:
y∝$\frac{q}{m}$
故$\frac{{y}_{H}}{{y}_{α}}=\frac{\frac{{q}_{H}}{{m}_{H}}}{\frac{{q}_{α}}{{m}_{α}}}=\frac{{q}_{H}}{{q}_{α}}×\frac{{m}_{α}}{{m}_{H}}=\frac{1}{2}×\frac{4}{1}=\frac{2}{1}$
(2)粒子做类似平抛运动,加速度为:
a=$\frac{qE}{m}$
根据分运动公式,有:
vx=v0
vy=at
tanθ=$\frac{{v}_{y}}{{v}_{x}}$
联立解得:
tanθ=$\frac{qEL}{m{v}_{0}^{2}}$
质子和α粒子以相同的初动能射入,故:
tanθ∝q
故质子和α粒子的偏转角度正切值之比为:
$\frac{tan{θ}_{H}}{tan{θ}_{α}}$=$\frac{{q}_{H}}{{q}_{α}}=\frac{1}{2}$
答:(1)质子和α粒子以相同的初速度v0射入时的侧向偏移量之比为2:1;
(2)质子和α粒子以相同的初动能射入时的偏转角度正切值之比为1:2.
点评 本题中带电粒子在偏转电场中做类平抛运动,其研究方法是运动的分解和合成,运用牛顿第二定律和运动学公式推导出偏角的正切是关键.

 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
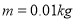 、电荷量
、电荷量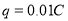 的带正电滑块从区域Ⅰ左侧与边界
的带正电滑块从区域Ⅰ左侧与边界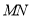 相距
相距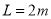 的
的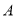 点以
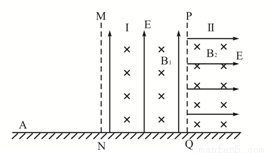
点以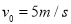 的初速度沿粗糙、绝缘的水平面向右运动,进入区域Ⅰ后,滑块立即在竖直平面内做匀速圆周运动,在区域Ⅰ内运动一段时间后离开磁场落回
的初速度沿粗糙、绝缘的水平面向右运动,进入区域Ⅰ后,滑块立即在竖直平面内做匀速圆周运动,在区域Ⅰ内运动一段时间后离开磁场落回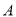 点。已知滑块与水平面间的动摩擦因数
点。已知滑块与水平面间的动摩擦因数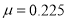 ,重力加速度
,重力加速度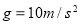 。
。
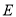 和区域Ⅰ中磁场的磁感应强度大小
和区域Ⅰ中磁场的磁感应强度大小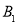 ;
;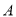 点出发到再次落回
点出发到再次落回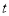 (可用分数表示,圆周率用字母
(可用分数表示,圆周率用字母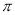 表示);
表示);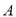 点以
点以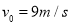 的初速度沿水平面向右运动,当滑块进入区域Ⅱ后恰好能做匀速直线运动,求有界磁场区域Ⅰ的宽度
的初速度沿水平面向右运动,当滑块进入区域Ⅱ后恰好能做匀速直线运动,求有界磁场区域Ⅰ的宽度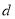 及区域Ⅱ内磁场的磁感应强度大小
及区域Ⅱ内磁场的磁感应强度大小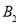 。(可用分数表示)。
。(可用分数表示)。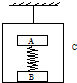 如图所示,木块A、B用轻弹簧相连,放在悬挂的木箱C内,处于静止状态,它们的质量之比是1:2:3.当剪断细绳的瞬间,各物体的加速度大小及其方向?
如图所示,木块A、B用轻弹簧相连,放在悬挂的木箱C内,处于静止状态,它们的质量之比是1:2:3.当剪断细绳的瞬间,各物体的加速度大小及其方向? 内存在水平向右的匀强电场,场强大小E=10N/c,在y≥0的区域内还存在垂直于坐标平面向里的匀强磁场,磁感应强度大小B=0.5T一带电量
内存在水平向右的匀强电场,场强大小E=10N/c,在y≥0的区域内还存在垂直于坐标平面向里的匀强磁场,磁感应强度大小B=0.5T一带电量 、质量
、质量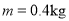 的小球由长
的小球由长 的细线悬挂于
的细线悬挂于 点小球可视为质点,现将小球拉至水平位置A无初速释放,小球运动到悬点
点小球可视为质点,现将小球拉至水平位置A无初速释放,小球运动到悬点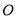 时,悬线突然断裂,此后小球又恰好能通过
时,悬线突然断裂,此后小球又恰好能通过 ),求:
),求:
 间的距离
间的距离 如图所示,物体A重40N,物体B重20N,A与B、A与地面间的动摩擦因数均为0.4,当用水平力F向右匀速拉动物体A时,试求:
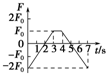
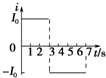
如图所示,物体A重40N,物体B重20N,A与B、A与地面间的动摩擦因数均为0.4,当用水平力F向右匀速拉动物体A时,试求: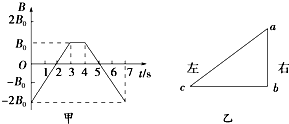 有一磁场方向竖直向下,磁感应强度B随时间t的变化关系如图5甲所示的匀强磁场.现有如图乙所示的直角三角形导线框abc水平放置,放在匀强磁场中保持静止不动,t=0时刻,磁感应强度B的方向垂直纸面向里,设产生的感应电流i顺时针方向为正、竖直边ab所受安培力F的方向水平向左为正.则下面关于F和i随时间t变化的图象正确的是( )
有一磁场方向竖直向下,磁感应强度B随时间t的变化关系如图5甲所示的匀强磁场.现有如图乙所示的直角三角形导线框abc水平放置,放在匀强磁场中保持静止不动,t=0时刻,磁感应强度B的方向垂直纸面向里,设产生的感应电流i顺时针方向为正、竖直边ab所受安培力F的方向水平向左为正.则下面关于F和i随时间t变化的图象正确的是( )