��Ŀ����
19���ھ�Եˮƽ���ϣ���һ����Ϊm=2.0��10-3kg�Ĵ����绬��A����������Ϊq=1.0��10-7C���ڻ���A�����?������һ�������硢����M=4.0��10-3kg�ľ�Ե����B��B����˽Ӵ��������ӣ��ڹ̶�����ֱǽ�ڵ��ᵯ���ϣ��ᵯ�ɴ�����Ȼ״̬������ԭ��s=0.05m����ͼ��ʾ����ˮƽ�����һˮƽ�������ǿ�糡���糡ǿ�ȵĴ�СΪE=4.0��105N/C������A�ɾ�ֹ�ͷź��������뻬��B������ײ������ײʱ�伫�̣���ײ������һ��ͬ�˶����ٶ�Ϊv=1m/s��������һ��ѹ����������̴����������ڣ�ʱ�����ɵĵ�������E0=3.2��10-3J���������������С���ƣ���ˮƽ���Ķ�Ħ������Ϊ��=0.50��Ħ������磬��ײ��ʧ�磬gȡ10m/s2����
��1������������ײǰ��˲ʱ������A���ٶȣ�
��2������A��ʼ�˶�λ���뻬��B�ľ���l��
��3��B���鱻���ɵ����������ǽ��������sm��
���� ��1��A��B��������ײ���̶����غ㣬��֪����Ĺ�ͬ�ٶȣ����ݶ����غ㶨�ɼ��������ǰA���ٶȣ�
��2��������ǰA�����ȼ����˶����̣����ö��ܶ��������l��
��3������A��Bһ��ѹ����������̣��赯��ѹ����Ϊx1���ɶ��ܶ���������õ���ѹ����������ѹ�������е糡���������������ܵļ��������ڵ糡�������Ĺ����跴����A��B������x2������ٶȼ�Ϊ�㣬�ɶ��ܶ������x2���Ƚϵ糡���뻬��Ħ�����Ĺ�ϵ���жϻ�����˶������������������룮
��� �⣺��1����A��B��ײǰA���ٶ�Ϊv1����ײ���̶����غ㣬�У�
mv1=��M+m��v
�������ݽ�ã�v1=3m/s
��2����A���ӿ�ʼ�˶�����ײB֮ǰ�����ݶ��ܶ������У�
qEl-��mgl=$\frac{1}{2}m{{v}_{1}}^{2}$-0
�������ݽ�ã�l=0.3m��
��3���赯�ɱ�ѹ�������ʱ��ѹ����Ϊs1����AB���壬������������ѹ����̹����У����������غ㶨�ɣ��У�
qEs1+$\frac{1}{2}��M+m��{v}^{2}$=��mg s1+E0����
�������ݽ�ã�s1=0.02m��
�赯�ɵ�һ�λָ���ԭ��ʱ��AB��ͬ����ΪEk�����������غ㶨�ɣ��У�
E0=qEs1+�̣�M+m��g s1+Ek ��
�ڵ��ɰ�BA�����Ƴ��Ĺ����У�����B�ܵ������Ħ����С��A�ܵ��������Ħ�����͵糡��֮�ͣ���������ֹ֮ͣǰ������û�зֿ���
���ɵ�һ�ν�AB����������ͬʱͬ��ֹͣʱ��B������ֱǽ����Զ�����ʱ���뵯��ԭ����Ϊs2�����ݶ��ܶ������У�
-qEs2-�̣�M+m��g s2=0-Ek ��
�٢��������������ݽ�ã�s2=0.03m
��B��ǽ�ڵ�������sm=s+s2=0.08m
��
��1������������ײǰ��˲ʱ������A���ٶ�Ϊ3m/s��
��2������A��ʼ�˶�λ���뻬��B�ľ���Ϊ0.3m��
��3��B���鱻���ɵ��������ֱǽ��������smΪ0.08m��
���� ������Ҫ�����˶��ܶ����Ͷ����غ㶨�ɵ�ֱ��Ӧ�ã�Ҫ�����Լ������������̣������������ɣ�����ۺ����������

 ����С״Ԫ��������������ϵ�д�
����С״Ԫ��������������ϵ�д�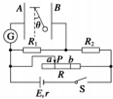 ��ͼ��ʾ��A��BΪ������ͬ����ֱ���õ�ƽ�н����壬�������������ʾ�Ե������һ����С����S�պϣ��һ����������Ļ���ͷP��a������ʱ��Ե������ƫ����ֱ����Ƚǣ���Դ�����費�ܺ��ԣ��������ж���ȷ���ǣ�������
��ͼ��ʾ��A��BΪ������ͬ����ֱ���õ�ƽ�н����壬�������������ʾ�Ե������һ����С����S�պϣ��һ����������Ļ���ͷP��a������ʱ��Ե������ƫ����ֱ����Ƚǣ���Դ�����費�ܺ��ԣ��������ж���ȷ���ǣ�������| A�� | ��A��ˮƽ���������ƶ��������ȽDZ�� | |
| B�� | ��B����ֱ�����ƶ������������������������ϵĵ��� | |
| C�� | ������ͷP��a��b����ʱ���ȽDZ�С | |
| D�� | ������ͷP��a��b����ʱ�����������д������µĵ��� |
| A�� | $\frac{\sqrt{{F}_{1}^{2}+{F}_{2}^{2}}}{2}$ | B�� | $\sqrt{\frac{{F}_{1}^{2}+{F}_{2}^{2}}{2}}$ | C�� | $\frac{\sqrt{{F}_{1}+{F}_{2}}}{2}$ | D�� | $\sqrt{\frac{{F}_{1}+{F}_{2}}{2}}$ |
 ��ͥ��·�и�յ�������Dz������ģ���ͼ��ʾ�������ò��ʱ����ߺ����ߵ�����ʹ�÷����У���ȷ���Ǽף�
��ͥ��·�и�յ�������Dz������ģ���ͼ��ʾ�������ò��ʱ����ߺ����ߵ�����ʹ�÷����У���ȷ���Ǽף� ��ͼ��ʾ��������һ���A��B��C����������ˮƽ��F�����¹�ͬ���ٶ�v��ˮƽ��������ֱ���˶�������B����������A��Ħ������С��0N������B����������C��Ħ������С��FN��
��ͼ��ʾ��������һ���A��B��C����������ˮƽ��F�����¹�ͬ���ٶ�v��ˮƽ��������ֱ���˶�������B����������A��Ħ������С��0N������B����������C��Ħ������С��FN�� ��ŵ����ҹ������о����ش�Ƽ���Ŀ��ԭ����������ģ��˵������ͼ����ʾ������MN�Ҳ������ֱ���ϵ���ǿ�ų����߳�ΪL�������ε��ѽ����߿�abcd���ڹ⻬ˮƽ���ϣ�����ΪR������Ϊm��ab���ڴų�������MN���߽߱磮t=0ʱ��Ÿ�Ӧǿ��B��ʱ��t�ı仯������B=B0+kt��kΪ������ij������������������Բ��ƣ�
��ŵ����ҹ������о����ش�Ƽ���Ŀ��ԭ����������ģ��˵������ͼ����ʾ������MN�Ҳ������ֱ���ϵ���ǿ�ų����߳�ΪL�������ε��ѽ����߿�abcd���ڹ⻬ˮƽ���ϣ�����ΪR������Ϊm��ab���ڴų�������MN���߽߱磮t=0ʱ��Ÿ�Ӧǿ��B��ʱ��t�ı仯������B=B0+kt��kΪ������ij������������������Բ��ƣ� ����ʱ��������������ʱ������������ʱ������ӽ����磨������ֱ���磩���ҹ�ʹ�ý������Ƶ����50Hz����ֽ����ÿ����������֮���ʱ����Ϊ0.02s�����ý���50Hz������Դ�ϵĴ���ʱ���ⶨС�����ȼ���ֱ���˶��ļ��ٶȵ�ʵ���У��õ���ͼ��ʾ��һ��ֽ�����ӱȽ������ĵ㿪ʼ��ÿ5����ӡ��ȡһ�������㣬�ֱ����0��1��2��3��4^����0��1�����ľ���s1=30mm��3��4�����ľ���s4=48mm����С����0��1�����ƽ���ٶ�Ϊ0.3m/s��С���ļ��ٶ�Ϊ0.6m/s2��
����ʱ��������������ʱ������������ʱ������ӽ����磨������ֱ���磩���ҹ�ʹ�ý������Ƶ����50Hz����ֽ����ÿ����������֮���ʱ����Ϊ0.02s�����ý���50Hz������Դ�ϵĴ���ʱ���ⶨС�����ȼ���ֱ���˶��ļ��ٶȵ�ʵ���У��õ���ͼ��ʾ��һ��ֽ�����ӱȽ������ĵ㿪ʼ��ÿ5����ӡ��ȡһ�������㣬�ֱ����0��1��2��3��4^����0��1�����ľ���s1=30mm��3��4�����ľ���s4=48mm����С����0��1�����ƽ���ٶ�Ϊ0.3m/s��С���ļ��ٶ�Ϊ0.6m/s2�� ���ᵯ��������������Ϊm��A��B����鶼��v���ٶ��ڹ⻬��ˮƽ�����˶������ɴ���ԭ��������ΪM�����C��ֹ����ǰ������ͼ��ʾ��B��C��ײ������ճ��һ���˶��������Ժ���˶��У���m��M���������Ĺ�ϵʱ��A���п��������˶���
���ᵯ��������������Ϊm��A��B����鶼��v���ٶ��ڹ⻬��ˮƽ�����˶������ɴ���ԭ��������ΪM�����C��ֹ����ǰ������ͼ��ʾ��B��C��ײ������ճ��һ���˶��������Ժ���˶��У���m��M���������Ĺ�ϵʱ��A���п��������˶���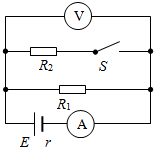 ��ͼ��ʾ��R1=18����������S�պ�ʱ���������Ķ���Ϊ1.5A����ѹ���Ķ���Ϊ9V��������S�Ͽ�ʱ������������Ϊ0.6A�������R2����ֵ�͵�Դ�綯�Ƽ����裮
��ͼ��ʾ��R1=18����������S�պ�ʱ���������Ķ���Ϊ1.5A����ѹ���Ķ���Ϊ9V��������S�Ͽ�ʱ������������Ϊ0.6A�������R2����ֵ�͵�Դ�綯�Ƽ����裮