题目内容
7. 如图所示,一质量为m=2kg的物体在一水平拉力F的作用下沿水平面运动,物体运动的v-t图象如图所示,已知物体与水平面的摩擦因数μ=0.2,g取10m/s2.求:
如图所示,一质量为m=2kg的物体在一水平拉力F的作用下沿水平面运动,物体运动的v-t图象如图所示,已知物体与水平面的摩擦因数μ=0.2,g取10m/s2.求:(1)拉力F的大小;
(2)前6s内拉力F所做的功.
分析 根据速度时间图线的斜率求出物体的加速度,根据牛顿第二定律求出拉力F的大小.
根据图线围成的面积求出位移,结合拉力的大小求出拉力做功的大小.
解答 解:(1)根据图象可知物体的加速度大小为
a=$\frac{v-0}{t}$=$\frac{12}{6}m/{s}^{2}$=2m/s2
根据牛顿运动定律得物体受到的摩擦力大小为
f=μmg=0.2×20N=4N
根据牛顿运动定律得拉力的大小为
F-f=ma
代入数据解得 F=8N
(2)由图象可得位移大小为
x=$\frac{1}{2}$vt=$\frac{1}{2}×12×6$m=36m
拉力所做的功为
W=Fx=8×36J=288J.
答:(1)拉力F的大小为8N;
(2)前6s内拉力F所做的功为288J.
点评 本题考查了牛顿第二定律和速度时间图线的综合运用,知道图线的斜率表示加速度,图线与时间轴围成的面积表示位移.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
2.物体沿直线运动的v-t关系如图所示,已知在第1秒内合外力对物体做的功为W,则( )
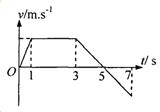

| A. | 从第1秒末到第3秒末合外力做功为4W | |
| B. | 从第3秒末到第5秒末合外力做功为-W | |
| C. | 从第5秒末到第7秒末合外力做功为W | |
| D. | 从第3秒末到第4秒末合外力做功为-0.25W |
12. 如图所示为节水灌溉设备喷水时的示意图.设备中的喷嘴距地高0.8m,假定水从喷嘴水平喷出,喷灌的地面区域半径为4m,不计空气阻力,取g=10m/s2.下列说法正确的是( )
如图所示为节水灌溉设备喷水时的示意图.设备中的喷嘴距地高0.8m,假定水从喷嘴水平喷出,喷灌的地面区域半径为4m,不计空气阻力,取g=10m/s2.下列说法正确的是( )
 如图所示为节水灌溉设备喷水时的示意图.设备中的喷嘴距地高0.8m,假定水从喷嘴水平喷出,喷灌的地面区域半径为4m,不计空气阻力,取g=10m/s2.下列说法正确的是( )
如图所示为节水灌溉设备喷水时的示意图.设备中的喷嘴距地高0.8m,假定水从喷嘴水平喷出,喷灌的地面区域半径为4m,不计空气阻力,取g=10m/s2.下列说法正确的是( )| A. | 水下落的加速度为8m/s2 | B. | 水从喷嘴到地面的时间为0.4s | ||
| C. | 水从喷嘴喷出后动能不变 | D. | 水从喷嘴喷出的速率为1m/s |
16. 如图所示,在固定的光滑斜面上,有一重量为G的物体在一水平推力F的作用下处于静止状态.若斜面的斜角为θ,则( )
如图所示,在固定的光滑斜面上,有一重量为G的物体在一水平推力F的作用下处于静止状态.若斜面的斜角为θ,则( )
 如图所示,在固定的光滑斜面上,有一重量为G的物体在一水平推力F的作用下处于静止状态.若斜面的斜角为θ,则( )
如图所示,在固定的光滑斜面上,有一重量为G的物体在一水平推力F的作用下处于静止状态.若斜面的斜角为θ,则( )| A. | F=Gtanθ | B. | F=Gsinθ | ||
| C. | 物体对斜面的压力FN=Gcosθ | D. | 物体对斜面的压力FN=Gsinθ |
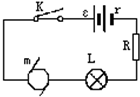 如图所示,已知电源电动势E=220V,内阻r=1Ω,当接入固定电阻R=4Ω时,电路中标有“3V 6W”的灯泡L和内阻r′=0.5Ω的小型直流电动机均恰能正常工作,求:
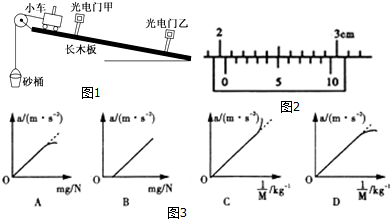
如图所示,已知电源电动势E=220V,内阻r=1Ω,当接入固定电阻R=4Ω时,电路中标有“3V 6W”的灯泡L和内阻r′=0.5Ω的小型直流电动机均恰能正常工作,求: 某同学用如图1所示的实验装置探究外力做功与小车动能变化的关系.
某同学用如图1所示的实验装置探究外力做功与小车动能变化的关系.