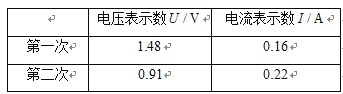
题目内容
【题目】一骑手在送餐途中需经过一段长为L=218m的水平直轨道,然后驶入一段半圆形的弯轨道。为尽快送餐,骑手需在最短时间通过直轨道。为了避免发生危险,直轨道上限速v1=144km/h,弯轨道上车速不得超过v2=72km/h,骑手电动车的启动加速度为a1=4m/s2制动加速度为a2=8m/s2，求骑手在直轨道上所用的最短时间。
某同学解法如下:v1=144km/h=40m/s,v2=72km/h=20m/s,为尽快通过直轨道,骑手应先由静止加速到最大速度v1=40m/s,然后再减速到v2=20m/s.
加速时间为
减速时间为
故所用最短时间为
你认为这位同学的解法合不合理,请完成计算;若不合理,请说明理由并用你自己的方法计算。
【答案】不合理.
【解析】
加速到速度达最大通过的位移
再减速到弯道允许的速度时通过的位移
，因此，如果按这种方式运动，电动车在弯道上行驶的速度将大于72km/h.
故这位同学的解法不合理.
正确解法：
电动车在直轨道上应从静止开始加速，当速度达到某一值(小于轨道允许的最大速度)时开始减速，恰好在运动直轨道末端时速度减为20m/s.
电动车匀加速运动的位移
匀减速运动的位移
得：
解得：或
(舍去)
练习册系列答案
字词句篇与同步作文达标系列答案
相关题目
