题目内容
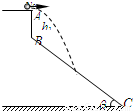
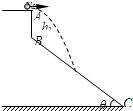 如图所示,BC是倾角为θ=37°的斜坡,AB竖直高度差hl=5m,一小球以初速度v0=14m/s水平飞出,最后飞落到BC上(不计空气阻力,g取10m/s2,sin37°=0.6,cos37°=0.8).求:
如图所示,BC是倾角为θ=37°的斜坡,AB竖直高度差hl=5m,一小球以初速度v0=14m/s水平飞出,最后飞落到BC上(不计空气阻力,g取10m/s2,sin37°=0.6,cos37°=0.8).求:(1)小球在空中飞行的时间t
(2)小球落在斜面上时的速度v.
分析:(1)平抛运动的在水平方向上做匀速直线运动,在竖直方向上做自由落体运动,抓住在斜面上水平位移和竖直位移的关系求出飞行的时间.
(2)根据速度时间公式求出小球竖直方向上的分速度,结合平行四边形定则求出落在斜面上时的速度大小.
(2)根据速度时间公式求出小球竖直方向上的分速度,结合平行四边形定则求出落在斜面上时的速度大小.
解答:解:(1)设在空中飞行时间为t,则有:x=v0t
y=
g?t2
tan370=
则tan370=
,
解方程得:∴t=2.5s (t=-0.4s舍去)
(2)小球落在斜面上时,竖直速度vy=gt=25m/s
小球落在斜面上时,速度为v=
=
m/s.
答:(1)小球在空中飞行的时间为2.5s.
(2)小球落在斜面上的速度为
m/s.
y=
| 1 |
| 2 |
tan370=
| y-h1 |
| x |
则tan370=
| ||
| vct |
解方程得:∴t=2.5s (t=-0.4s舍去)
(2)小球落在斜面上时,竖直速度vy=gt=25m/s
小球落在斜面上时,速度为v=
|
| 821 |
答:(1)小球在空中飞行的时间为2.5s.
(2)小球落在斜面上的速度为
| 821 |
点评:解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,抓住位移关系,结合运动学公式进行求解.

练习册系列答案
相关题目
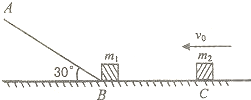 如图所示,AB是倾角为30°足够长的光滑斜面,BC是足够长的光滑水平面,且在B点与斜面平滑连接,质量m1=0.2kg的滑块嚣于B点,质量m2=0.1kg的滑块以v0=9m/s速度向左运动并与m1发生撞碰,碰撞过程中没有机械能损失,且ml通过B点前后速率不变,将滑块视为质点,以下判断正确的是(g=10m/s2)( )
如图所示,AB是倾角为30°足够长的光滑斜面,BC是足够长的光滑水平面,且在B点与斜面平滑连接,质量m1=0.2kg的滑块嚣于B点,质量m2=0.1kg的滑块以v0=9m/s速度向左运动并与m1发生撞碰,碰撞过程中没有机械能损失,且ml通过B点前后速率不变,将滑块视为质点,以下判断正确的是(g=10m/s2)( ) 如图所示,AB是倾角θ为45°的直轨道,CD是半径R=0.4m圆弧轨道,它们通过一段曲面BC平滑相接,整个轨道处于竖直平面内且处处光滑.一个质量m=1kg的物体(可以看作质点)从高H的地方由静止释放,结果它从圆弧最高点D点飞出,垂直斜面击中P点.已知P点与圆弧的圆心O等高.求:(取g=10m/s2)
如图所示,AB是倾角θ为45°的直轨道,CD是半径R=0.4m圆弧轨道,它们通过一段曲面BC平滑相接,整个轨道处于竖直平面内且处处光滑.一个质量m=1kg的物体(可以看作质点)从高H的地方由静止释放,结果它从圆弧最高点D点飞出,垂直斜面击中P点.已知P点与圆弧的圆心O等高.求:(取g=10m/s2)