题目内容
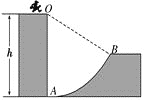
【题目】如图所示，水平地面上不同位置的三个小球斜上抛，沿三条不同的路径运动最终落在同一点，三条路径的最高点是等高的，若忽略空气阻力的影响，下列说法正确的是（ ）
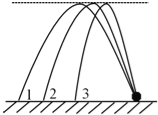
A. 沿路径1抛出时的小球落地的速率最大
B. 沿路径3抛出的小球在空中运动时间最长
C. 三个小球抛出的初速度竖直分量相等
D. 三个小球抛出的初速度水平分量相等
【答案】AC
【解析】试题分析：三个小球都做斜抛运动，运用运动的分解法，将其运动分解为竖直和水平两个方向研究，水平方向做匀速直线运动，竖直方向做竖直上抛运动，根据运动学公式列式，再进行分析．
解：设任一小球初速度大小为v0，初速度的竖直分量为vy，水平分量为vx，初速度与水平方向的夹角为α，上升的最大高度为h，运动时间为t，落地速度大小为v．
A、C、D、取竖直向上方向为正方向，小球竖直方向上做匀减速直线运动，加速度为a=﹣g，由0﹣
=﹣2gh，得：
vy=
，h相同，vy相同，则三个小球初速度的竖直分量相同．
由速度的分解知：vy=v0sinα，由于α不同，所以v0不同，沿路径1抛出时的小球的初速度最大．
根据机械能守恒定律得知，小球落地时与抛出时速率相等，所以可知三个小球落地时的速率不等，也是沿路径1抛出时的小球的初速度最大．
又有 vy=vxtanα，vy相同，α不同，则vx不同，初速度水平分量不等，故A正确，C正确，D错误．
B、由运动学公式有：h=
g（
）2，则得：t=2
，则知三个球运动的时间相等；故B错误．
故选：AC．
练习册系列答案
课堂练加测系列答案
轻松课堂单元测试AB卷系列答案
相关题目
